|
BAB II
LANDASAN TEORI
2.1. Zero knowledge proof
Zero knowledge proof adalah konsep yang sangat populer dan banyak
digunakan dalam sistem kriptografi. Dalam konsep ini, ada dua pihak yang
terlibat yaitu prover dan verifier. Pada awalnya Zero knowledge proof dikenalkan
dan dipublikasikan oleh (Jacques, Guilou, & Berson, 1990)pada paper yang
berjudul “How to Explain Zero-Knowledge Protocols to Your Children”. Dengan
teknik ini memungkinkan seorang prover menunjukkan bahwa dia memiliki hak
atau bukti ( credential ) tanpa harus menunjukkan nilai yang sebenarnya kepada
verifier. Zero knowledge proof banyak digunakan untuk sistem otentikasi karena
memiliki sifat – sifat sebagai berikut :
a. Completeness : Jika pernyataan tersebut memang benar, maka verifier
akan dapat membuktikan pernyataan itu benar secara berulang-ulang.
b. Soundness : Jika pernyataan itu salah, tidak akan ada kecurangan yang
dapat dilakukan prover untuk dapat meyakinkan verifier bahwa
pernyataan tersebut benar. Kecuali dengan beberapa kemungkinan kecil.
c. Zero-knowledge : Jika pernyataan itu benar, tidak akan ada
pengetahuan apapun yang didapatkan selain fakta tersebut. Hal ini
ditunjukkan dengan sebuah simulasi yang menunjukkan bahwa
pernyataan itu benar dan tidak ada yang diperoleh verifier dari prover.
7
|
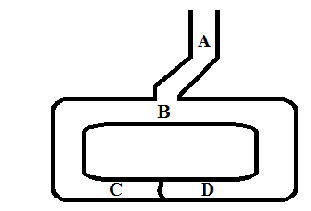 8
Jean Jacques Q dan Louis Guillou mengilustrasikan zero-knowledge proof
dengan menggunakan sebuah cerita tentang goa yang memiliki rahasia. Dalam
ilustrasi ini dikenal dua orang tokoh Peggy ( prover ) dan Victor ( verifier ).
Gambar 2.1–Ilustrasi Zero knowledge proof
Pada gambar 2.1 merupakan ilustrasi dari Zero Knowledge Proof,
Seseorang yang mengetahui kata kunci dapat membuka pintu rahasia antara C dan
D. Misalkan Peggy ingin membuktikan kepada Victor bahwa dia mengetahui kata
kunci untuk membuka pintu rahasia, maka yang perlu Peggy dan Victor lakukan
adalah sebagai berikut:
a. Victor berdiri di titik A
b. Peggy berjalan masuk kedalam gua menuju titik C atau D
c. Setelah Peggy tidak terlihat di dalam gua, Victor berjalan ke titik B
d. Victor kemudian memerintahkan kepada Peggy untuk :
1. Keluar dari jalur sebelah kiri atau sebelah kanan
2. Peggy kemudian akan merespon, dan menggunakan kata kunci yang
ia miliki untuk membuka pintu rahasia, jika seandainya ia benar-
benar punya.
|
|
9
3. Peggy dan Victor kemudian akan mengulangi langkah – langkah
tersebut sampai n kali.
Dengan metode ini, Victor tidak akan mungkin meyakinkan pihak ketiga
tentang bukti kepemilikan rahasia oleh Peggy dan dia juga tidak dapat
memperoleh informasi apapun tentang informasi rahasian yang diketahui oleh
Peggy. Hal ini mengakibatkan tidak mungkin Peggy dapat menebak secara tepat
secara terus menerus sisi sebelah mana Victor akan meminta keluar. Probabilitas
Peggy dapat menebak dengan secara tepat seperti ini akan sangat kecil apabila
dilakukan secara berulang-ulang(Schneier, 1996).
2.2. Zero Knowledge Proof of Knowledge Discrete
Logarithms
Dalam penerapan ZeroKnowledge Proof dilakukan dengan perhitungan
matematika, salah satunya dengan perhitunganDiscreteLogarithms. Pada paper
“Implementing Zero-Knowledge Authentication with Zero Knowledge
(ZKA•wzk)”(Brandon, 2010) membahas teknik tersebut yang digunakan untuk
authenticationweb dengan perhitunganDiscreteLogarithms. Algoritma ini
berlandaskan dari (Camenisch, 1998) Zero Knowledge Proof of Knowledge
Sigma Protocol menggunakan SPK1{(x) : Y = g0x}. Dengan tiga proses sebagai
berikut :
a. Inisialisasi :
1. Diketahui sebuah Group G dan g0,g1didapatkan dari random
element dari G.
2. Maka G dan g0menjadi public key.
|
|
10
b. Registrasi :
1. Usermemasukkanusername dan password
2. Kemudian password di hashing dengan fungsi hash. Diperoleh x =
hashing( password )
3. User melakukan perhitungan untuk Y = g0x
4. Kemudian user mengirim (username,Y)ke server
5. Server menyimpan username,Y
c. Authentication Process :
1. Servermelakukangenerate random variabel a, menyimpannya dan
mengirimkannya ke client
2. User memasukkan username dan password
3. Clientmelakukan hash ke password dengan fungsi hash, dan
menghitung x = hash(password)
x
4. Client menghitung Y = g0
5. Client melakukan generaterandom rx € G dan hitung T1 = g0rx
6. Client menghitung c=hash(Y,T1,A) dan zx=rx-c.x
7. Client mengirim (c, zx) ke Server
8. Servermenghitung T1= Ycg0zx dan mencocokkan c = c2, (c2 =
hash(Y,T2,A))
9. Jika sesuai, maka user telah di otentikasi
Teknik Zero Knowledge Proof merupakan teknik umum yang digunakan
untuk membuktikan pengetahuan tentang variable yang berkaitan dengan
password. Berikut penjelasan pada tabel 2.1 untuk setiap komponen yang
digunakan dalam algoritma ini :
|
 11
Tabel 2.1 – Penjelasan komponen Zero Knowledge Authentication
Component Description
G Merupakan serangkaian angka yang berdasarkan pada formula.
Kumpulan angka ini bersifat public dan dapat diakses oleh
kedua pihak , Client ( Prover ) danServer ( Verifier ).
g0 Sebuah angka yang diperoleh dari G dan merupakan elemen
dari G. Variabel ini bersifat public dan dapat diakses oleh
kedua pihak ( prover dan verifier ).
x Hasil hash dari password yang di-input oleh prover.
Y Sebuah aliaspassword dari prover. Digunakan verifier untuk
menghitung proof of knowledge.
A Randomtoken yang di-generate setiap provermelakukan login.
T1,T2,rx,zx,c,c2 Variabel lainnya yang digunakan dalam kalkulasi.
Legend :
Nilai public – Diketahui oleh prover dan verifier.
Nilai rahasia server – Tetapi dapat diturunkan kepada prover ( client ).
Nilai rahasia client – Hanya diketahui oleh prover ( client ).
Dengan pengetahuan tentang variable yang berkaitan dengan password
tersebut, maka algoritma dapat bekerja. Untuk menjalankan algoritma maka G
harus di-generate dari sebuah angka seperti {1,2,3,4,..}, dan g0didapatkan dari
hasil random angka dalam G. Algoritma itu menggunakan g0yang berasal dari G
sehingga sulit mendapatkan perhitungan logaritma diskrit. Setiap komponen pada
|
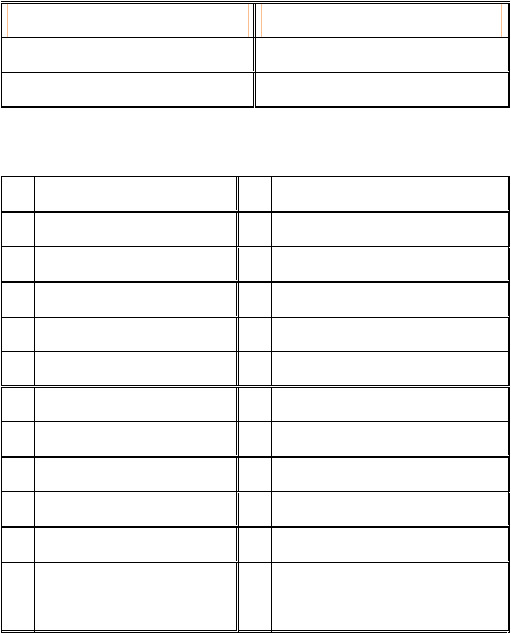 12
pada tabel 2.2 diperlihatkan komponen - komponen yang dimiliki client dan
server.
Tabel 2.2 – Nilai yang dimiliki pada proses authentication
Prover ( User )
Verifier ( Server )
g0
g0
Password
Y
Tabel 2.3 – Proses authentication
No User (Prover) Verifier (Server)
1
Menghasilkan random A
2 Menerima A Kirim A
3 Hitung x = hash (password)
4 Hitung Y = g0x
5 Menghasilkan random rx
6 Hitung T1 = g0rx
7 Hitung c = hash(Y, T1, A)
8 Hitung zx = rx – c.x
Terima c, zx
9 Kirim c, zx
10
Hitung T2 =Ycg0zx
11
bandingkan jika c = c2, (c2 =hash(Y,
T2,A) )
algoritma Zero Knowledge Proof ini diterapkan dalam sistem client dan server,
|
|
13
Dari formula perhitungan yang dilakukan di tabel 2.3, diketahui T1dihitung
tanpa mengetahui pengetahuan apapun karena rxdiperoleh dari hasil random.
Diperoleh persamaan sebagai berikut :
d. Langkah 6 : T1= g0rx
e. Langkah 10 : T1 =Yc g0zx
f. Maka diperoleh persamaan : g0rx= Yc g0zx
g. Langkah 4 : Y = g0x
h. Langkah 8 : zx= rx– c.x
i. Lakukan subtitusi :
g0rx= Ycg0zx
g0rx= (g0x)cg0(rx-cx)
g0rx= g0cxg0rx-cx
g0rx= g0cx+rx-cx
g0rx= g0rx( Diterima )
Dari persamaan tersebut diketahui, dengan ketiga elemen tersebut maka
dapat dibuktikan bahwa c = c2 dan user mengetahui nilai x.
2.3. Keamanan komputer
Keamanan komputer adalah sebuah konsep dan metode untuk melindungi
sumber daya yang sensitif dalam sistem komputer(Gollmann, 2010). Keamanan
komputer juga meliputi kebijakan yang mengatur akses ke data atau informasi
yang dilindungi atau bersifat privacy. Dalam dunia teknologi, keamanan komputer
difokuskan pada mekanisme untuk mengaturkebijakan penggunaan data atau
informasi tersebut. Dalam kebijakan penggunaan data atau informasi ini,
|
|
14
diperhatikan. Keamanan komputer dan keamanan jaringan adalah masalah penting
yang saling terkait dan tidak dapat dipisahkan. Permasalahan dalam keamanan
jaringan atau cyber securitytidak hanyamelindungi sistem yang digunakan untuk
menyimpan data seperti data tentang warga negara , perusahaan, atau instansi
pemerintah dan data lain-lainnya tetapi infrastruktur jaringan , router , nama
domainserver , dan switch yang membentuk sistem ini tidak boleh memiliki
kendala dan permasalahan , atau komputer tidak akan lagi dapat berkomunikasi
secara akurat atau dapat dipercaya(Bishop, 2003). Dapat disimpulkan keamanan
komputer harus meliputi :
a. Keamanan data pada komputer itu sendiri
b. Keamanan data pada komputer pada saat transmisi
Sebuah komputer saat ini membutuhkan sebuah jaringan untuk saling
bertukar data dan informasi. Data pada jaringan tersebut dapat bersifat umum dan
dapat bersifat rahasia. Untuk itu diperlukan suatu metode untuk menjaga
keamanan data tersebut. Keamanan jaringan komputer dibagi menjadi empat
bidang yang saling terkait, yaitu kerahasiaan, keaslian, pengakuan, dan kontrol
integritas(Kristanto, 2007). Kerahasiaan dilakukan untuk menjauhkan data atau
informasi dari orang-orang yang tidak berhak. Keaslian dilakukan untuk menjaga
dan me mastikan identitas sebelum memberikan data atau informasi ke tujuan.
Pengakuan dilakukan untuk memastikan data atau informasi tidak dapat
disangkal, sedangkan kontrol integritas dilakukan untuk menjaga konsistensi yang
mengacu pada sumber data yang belum pernah di manipulasi ( utuh ).
keamanan jaringanatau cybersecuritymerupakan salah satu faktor yang harus
|
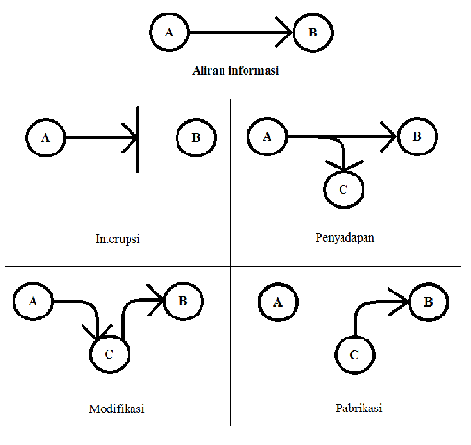 15
Banyak cara yang digunakan oleh orang lain untuk memperoleh informasi,
baik secara legal maupun tidak legal. Berbagai cara tersebutdilakukan untuk
memperoleh data yang bersifat rahasia. Bentuk – bentuk usaha orang yang tidak
berhak untuk mengambil informasi tersebut terlihat seperti pada gambar 2.2.
Gambar 2.2 – Berbagai bentuk jenis serangan jaringan
Dari gambar 2.2 ta mpak ada empat golongan usaha melakukan serangan
terhadap informasi yaitu :
a. Interupsi
|
|
16
Dalam model ini aliran informasi diputus sehingga penerima tidak
memperoleh informasi yang ditujukan kepadanya. Contoh usaha ini
adalah dengan memotong saluran komunikasi.
b. Penyadapan
Dalam model ini ada pihak lain yang tidak dikenal ikut serta dalam
komunikasi. Contoh usaha ini adalah dengan melakukan sniffing pada
saluran komunikasi dan kemudian menyalin informasi yang ada.
c. Modifikasi
Dalam model ini tidak hanya ikut mendengarkan informasi tetapi juga
melakukan perubahan dan mengirimkan hasil perubahan tersebut ke
tujuan sebenarnya. Contoh usaha ini adalah mengubah data atau program
yang akan dikirim.
d. Pabrikasi
Dalam model ini pihak yang tidak bertanggung jawab mengirimkan
informasi ke tujuan, walaupun sebenarnya pengirim yang asli tidak
mengirimkan informasi. Contoh usaha ini adalah dengan mengirimkan
pesan ke pengguna dalam jaringan dengan identitas orang lain.
2.3.1. Kriptografi
Kriptografi berasal dari bahasa Yunani, crypto dan graphia. Crypto berarti
rahasia dan graphia berarti tulisan. Menurut terminologinya, kriptografi adalah
ilmu dan seni untuk menjaga pesan ketika pesan dikirim dari suatu tempat ke
tempat lain(Ariyus, 2008). Pengertian kriptografi adalah teknik yang digunakan
untuk mengubah teks asli (plaintext) dengan menggunakan suatu kunci tertentu
|
|
17
Arisandi, 2012). Proses ini lebih dikenal dengan istilah enkripsi. Selanjutnya,
chipertext yang ada dapat diubah menjadi teks asli semula dengan metode yang
dikenal dengan istilah dekripsi.Adapun empat tujuan mendasar dari kriptografi
adalah:
a. Confidentiality adalah layanan yang ditujukan untuk menjaga agar pesan
tidak dapat dibaca oleh pihak-pihak yang tidak berhak.
b. Data integrity adalah layanan yang menjamin bahwa pesan masih
asli/utuh atau belum pernah dimanipulasi selama pengiriman.
c. Authentication adalah layanan yang berhubungan dengan identifikasi,
baik mengidentifikasi kebenaran pihak-pihak yang berkomunikasi
(userauthenticationatauentityauthentication) maupun mengidentifikasi
kebenaran sumber pesan (dataoriginauthentication).
d. Non-repudiation adalah layanan untuk mencegah entitas yang
berkomunikasi melakukan penyangkalan. Sebagai contoh apabila entitas
A melakukan pengiriman ke B , maka harus dapat dipastikan A tidak
dapat menyangkal bahwa A tidak melakukan pengiriman data ke B dan
juga sebaliknya untuk B bila menyangkal tidak menerima data yang
dikirim A.
2.3.2. Enkripsi dan Dekripsi
Menurut (Soewito, Vespa, & Weng, 2008) salah satu cara untuk
memfasilitasi komunikasi pribadi (transmisi data) adalah dengan mengubah
informasi menggunakan enkripsi. Namun, algoritma enkripsi adalah operasi yang
menjadi sebuah kode-kode yang tidak dimengerti (chipertext)(Reza, Budiman, &
|
|
18
keterbatasan sumber daya komputasi dan batasan energi. Memilih algoritma
enkripsi-dekripsi yang cocok merupakan keputusan penting yang perlu dilakukan
dalam mengamankan pertukaran informasi tanpa memanfaatkan sumber daya
lebih, baik pada processor dan memory. Pada dasarnya enkripsi adalah proses
mengubah plaintext ( text yang dapat dibaca dan dimengerti manusia ) menjadi
ciphertext ( text yang tdak dapat dibaca dan dimengerti manusia ), sedangkan
dekripsi adalah proses mengubah kembali dari ciphertext ke plaintext semula.
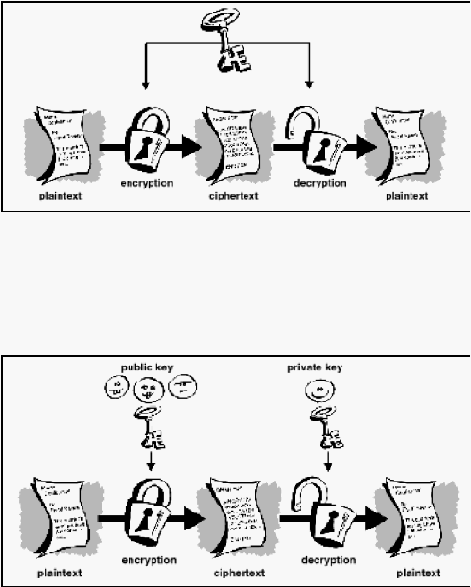
Enkripsi dan dekripsi dapat dikelompokkan menjadi dua bagian yaitu metode
konvensional ( secret key ) dan metode kunci publik ( public key ). Metode
konvensional ini menggunakan kunci untuk enkripsi dan dekripsi yang sama dan
rahasia yang hanya diketahui oleh pengirim dan penerima terlihat pada gambar
2.3, sedangkan metode kunci publik menggunakan dua kunci rahasia yaitu kunci
pertama ( kunci publik / public key ) digunakan untuk proses enkripsi dan kunci
kedua ( kunci pribadi / private key ) digunakan untuk proses dekripsi. Kunci
pertama bersifat umum, terbuka sehingga setiap orang dapat mengetahuinya.
Sedangkan kunci kedua sifatnya rahasia terlihat pada gambar 2.4. Beberapa
contoh enkripsi dan dekripsi yang menggunakan masing-masing metode tersebut
yaitu :
a. Metode Konvensional : AES, DES , Triple Des, Serpent dan lain-lainnya.
harus dilakukan dengan komputasi matematika dan operasi tertentu yang memiliki
|
 19
Gambar 2.3 – Enkripsi dan dekripsi dengan metode konvensional
b. Metode Public Key : RSA, Diffie-Hellman key, DSS, ElGamal dan lain-
lainnya.
Gambar 2.4 – Enkripsi dan dekripsi menggunakan metode public key
Pada masing-masing metode memiliki kelemahan dan kelebihan masing-
masing. Pada metode konvensional, masalah utama metode ini yaitu bagaimana
cara mengirimkan kunci simetris tersebut dari pengirim kepada penerima, bila
kunci sampai jatuh ke tangan orang yang tidak berhak maka metode pengamanan
ini menjadi tak berguna (Tjiharjadi & Wijaya, 2009). Pada metode publickey, hal
|
 20
metode pengamanan ini menjadi tak berguna, namun hal tersebut hanya berlaku
untuk privatekey, sedangkan publickey tidak. Metode ini juga memerlukan waktu
tambahan untuk pencarian publickey apabila pengirim ingin mengirimkan data
kepada lebih dari satu pengirim.
2.3.3. Key management
Menurut Menezes , et. al. (2010) salah satu solusi untuk menggunakan
teknik simetris key yang baik adalah dengan melibatkan entitas lain dalam sebuah
jaringan yang dapat dipercaya oleh semua entitas lainnya. Entitas tersebut
merujuk kepada pihak ketiga terpercaya yang disebut TrustedThirdParty. Jika dua
buah entitas ingin berkomunikasi maka Trusted Third Party menghasilkan kunci k
( session key ) dan mengirimkan kunci ke masing-masing entitas dalam bentuk
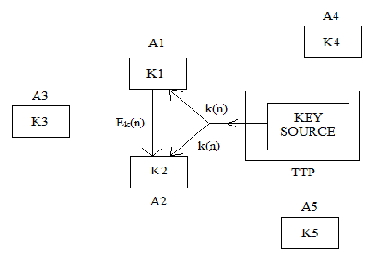
yang telah terenkripsi seperti pada gambar 2.5 untuk entitas A1 dan A2.
Gambar 2.5 – Key management menggunakan Trusted Third Party
yang sama juga terjadi jika sampai privatekey jatuh ke tangan orang lain maka
|
|
21
Pada gambar 2.5, entitas A1 akan mengirim data kepada entitas A2,
selanjutnya pihak A1 akan merequest sessionkey untuk ke y enkripsi dan dekripsi
yang telah di enkripsi dikirimkan ke entitas A1 dan entitas A2, yang selanjutnya
key tersebut di dekripsi menggunakan secretkey dan digunakan untuk meng-
enkripsi data yang akan dikirim ke entitas A1.
Keuntungan menggunakan metode ini yaitu :
a. Memudahkan dalam pengaturan entitas dalam jaringan
b. Setiap entitas hanya yang ingin berkomunikasi hanya menyimpan satu
buah secretkey yang diberikan TTP.
Kekurangan menggunakan metode ini yaitu :
a. Semua komunikasi membutuhkan komunikasi terdahulu dengan TTP.
b. TTP harus menyimpan sejumlah n secretkey.
c. TTP dapat membaca seluruh message.
d. Jika TTP diserang, maka semua komunikasi menjadi tidak aman.
2.4. Advanced Encryption System
Pada tahun 1997, National Institute of Standard and Technology (NIST) of
United States mengeluarkan Advanced Encryption Standard ( AES ) untuk
menggantikan Data Encryption Standard ( DES ). AES dibangun dengan maksud
untuk mengamankan pemerintahan di berbagai bidang. Pada tahun 1998, NIST
mengumumkan bahwa ada 15 proposal AES yang telah diterima dan dievaluasi,
setelah mengalami proses seleksi terhadap algoritma yang masuk, NIST
mengumumkan pada tahun 1999 bahwa hanya ada 5 algoritma yang diterima,
algoritma tersebut adalah :
|
 22
1. MARS
2. RC6
3. Rijndael
4. Serpent
5. Twofish
Setiap algoritma tersebut menjalani berbagai macam uji coba. Pada bulan
oktober 2000, NIST mengumumkan bahwa Rijndael sebagaialgoritma yang
terpilih untuk standar AES yang baru. Baru pada februari2001 NIST mengirimkan
list kepada Federal Information ProcessingStandards (FIPS) untuk standar AES.
Kemudian pada 26 November 2001,NIST mengumumkan produk akhir dari
Advanced Encryption Standard(Daemen & Rijmen, 2002). Pada table 2.4
diperlihatkan perbedaan variasi dari masing-masing algoritma yang diajukan.
Tabel 2.4–Perbedaan variasi algoritma kelima finalis
Nama Algoritma Variasi
MARS Key Size 4-39 32-bit words
RC6 Word size w, no. of rounds r, key size 0-255 bytes
Rijndael Block length of 128, 192, or 256 bits
Serpent Key size 0..256 bits
Twofish Key size 0..32 bytes
NIST akhirnya mengumumkan algoritma Rijndael memiliki tingkat
keamanan yang baik, performa, effisien, dapat diterapkan dan fleksibilitas yang
baik. Algoritma Rijndael dikembangkan oleh John Daemen dan Vincent Rijmen
|
|
23
2011) AES encryption sangat efisien digunakan baik pada hardware maupun
implementasi software, memiliki keamanan yang baik dan tingkat kecepatan yang
tinggi, dalam penerapan pada hardware pun sangat berguna terutama pada
wireless security seperti komunikasi militer dan mobile telephone.
Hasil evaluasi akhir didapat dari masukan masyarakat di seluruh dunia yang
didasarkan pada tiga karakteristik yaitu :
1. Security
Mencakup ketahanan terhadap serangan, kompleksitas matematika,
keac akan hasil output dan keamanan dibandingkan dengan algoritma
lain.
2. Cost
Mencakup kecepatan enkripsi, memori yang diperlukan, dan tidak ada
perjanjian lisensi yaitu algoritma harus tersedia secara gratis tanpa royalti
di seluruh dunia.
3. Algorithm and implementation characteristics
Algoritma harus dapat diterapkan dalam berbagai perangkat keras dan
sistem perangkat lunak, dan algoritma harus relatif sederhana.
Setelah dilakukan tinjauan yang ekstensif terhadap algoritma Rijndael maka
algoritma Rijndael dipilih sebagai algoritma untuk AdvancedEncryptionSystem (
AES ).
dari universitas Katholieke di Leuven. Menurut (Karthigaikumar & Rasheed,
|
 24
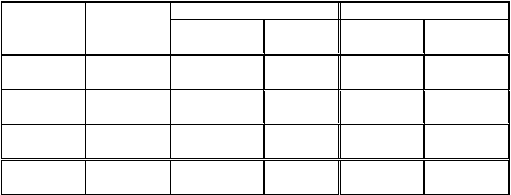
Tabel 2.5 – Perbandingan keamanan dan kecepatan ke empat finalis
(Perikamana, 2013)
Speed Memory
Algorithm
Security
Encryption /
Key RAM ROM
Decryption
RC6 Adequate High End Average Average Average
Rijndael Adequate High End High End High End High End
Serpent High Low End Average Average Average
Twofish High Average High End High End Average
Pada tabel 2.5 diperlihatkan perbandingan keamanan dan kecepatan dari
para finalis, perbandingan tersebut hanya membandingkan keempat finalis yang
dilakukan oleh Perikamana pada tahun 2013.
2.4.1. Algoritma Rijndael
Algoritma Rijndael merupakan algoritma cryptography yang dapat
digunakan untuk mengamankan data. Algoritma Rijndael adalah blok ciphertext
simetrik yang dapat mengenkripsi dan dekripsi informasi.Algoritma ini sangat
fleksibel karena dapat menggunakan kunci kriptografi 128 bit , 192 bit atau 256
bit untuk mengenkripsi dan dekripsi data pada blok 128 bits(Krishnamurthy &
Ramaswamy, 2008). Dari 128 Bits data tersebut dibagi kedalam 16 bytes,
kemudian setiap byte dipetakan kedalam sebuah matrix berukuran 4x4 yang
disebut state. Seluruh operasi yang dilakukan oleh algoritma ini akan dilakukan
pada state tersebut. Algoritma rijndael ini menggunakan numberofRounds (Nr)
|
 25
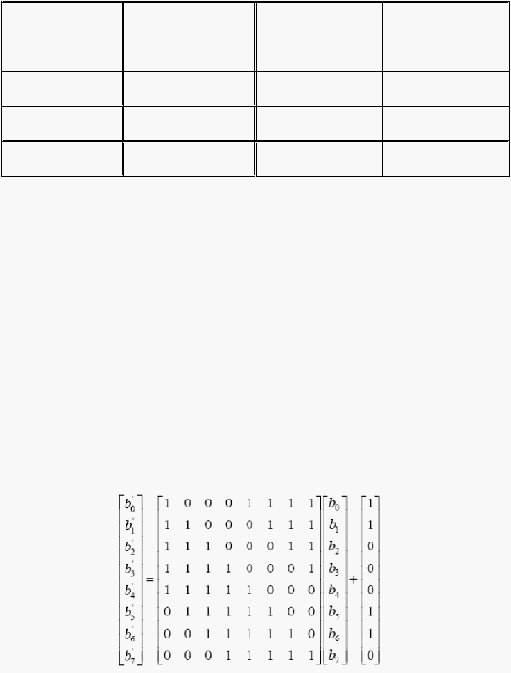
seperti pada tabel 2.6.
Tabel 2.6 – Perbandingan panjang key algoritma AES
AES Algorithm Input/Output Size
Key length
Number of
Block size (Nb)
Nk
rounds Nr
AES - 128 4 Words 4 Words 10 rounds
AES - 192 4 Words 6 Words 12 rounds
AES - 256 4 Words 8 Words 14 rounds
Algoritma ini melakukan empat byte-orientedcryptographytransformation
yaitu :
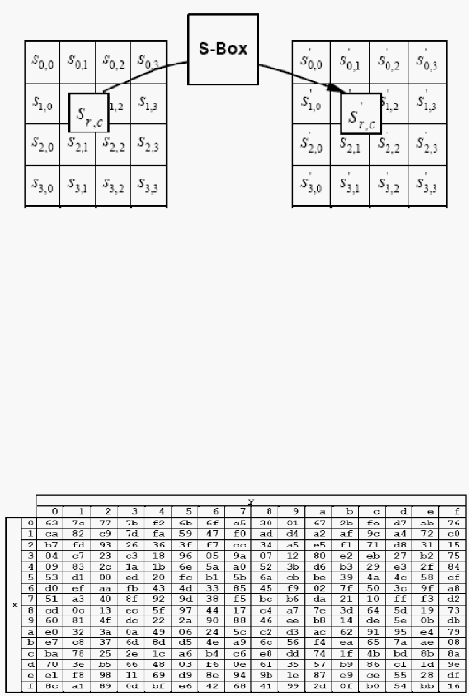
a. Subtitusibyte transformation
Operasi penukaran byte secara nonlinear menggunakan tabel subtitusi S-
box pada masing-masing blok state. Tabel S-box bersifat dapat
dikembalikan ke semula setelah disubtitusi dan tabel S-box dibangun
oleh dua komposisi transformasi.Dalam bentuk matriks, elemen S-box
dapat dinyatakan seperti pada gambar 2.6.
Gambar 2.6 – Bentuk matriks elemen S-box
pada saat eksekusi tergantung pada ukuran panjang kunci yang digunakan
|
 26
Dari subtitusi elemen pada matriks data ( state ) dengan tabel S-box maka
efek perubahan bentuk yang didapat seperti pada gambar 2.7.
Gambar 2.7– Ilustrasi subtitusi state dengan tabel S-box
S-box digunakan pada transformasi subtitusi byte dalam bentuk bilangan
hexadecimal, Sebagai contoh, jika S1,1= {53}, kemudian nilai subtitusi
akan ditentukan oleh persimpangan antara baris (x) dengan index ‘5’ dan
kolom (y) dengan index ‘3’, seperti terlihat pada tabel S-Box pada
gambar 2.8. Maka hasil subtitusi byte tersebut akan menghasilkan S1,1=
{ed}.
Gambar 2.8– Tabel S-box untuk subtitusi byte transformation
|
 27
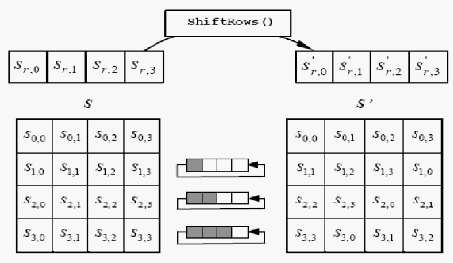
b. Shiftrows transformation
Pada transformasi shiftrows, byte blok pada ketiga baris terakhir digeser
sebanyak offset, sedangkan byte pada baris pertama tidak mengalami
pergeseran.
S’r,c= Sr,(c+shift(r,Nb)) mod NbUntuk 0 < r < 4 dan 0 = c < Nb
Pergeseran byte tergantung pada nilai tiap baris r, sebagai contoh untuk
Nb = 4 pada gambar 2.9.
Shift(0,4) = 0; bergeser 0 langkah atau tidak bergeser
Shift(1,4) = 1; bergeser 1 langkah
Shift(2,4) = 2; bergeser 2 langkah
Shift(3,4) = 3; bergeser 3 langkah
Pergeseran kolom pada setiap baris dilakukan dari kolom depan ke
kolom belakang dan kolom sebelumnya akan maju kedepan, ilustrasi
pada gambar 2.9 memperlihatkan proses shiftrows dilakukan.
Gambar 2.9 – Pergeseran blok state dengan operasi shiftrows
|
 28
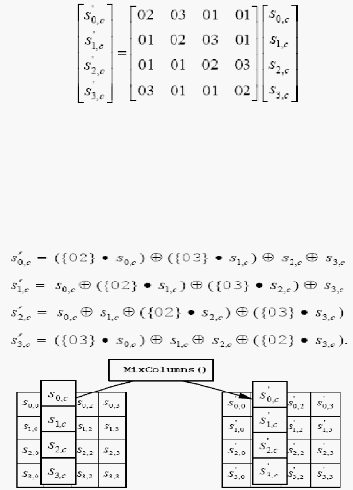
c. MixColumns transformation
Transformasi Mixcolumns digunakan untuk mencampur kolom dari
matrik state, kolom direpresentasikan sebagai polinomial Galois Field
GF(28). Output dari transformasi mixcolumns s’(x), seperti pada
persamaan berikut :
s’(x) = a(x) s(x) mod (x4 + 1)
Dimana a(x) = 03x3 + 01x2 + 01x1 + 02, persamaan ini dapat dipetakan
ke dalam bentuk matriks seperti pada gambar 2.10.
Gambar 2.10 – Matriks Rijndael’s Galois Field
Untuk 0 = c < Nb, Hasil perkalian pada matrik tersebut dapat dilihat
seperti pada persamaan dari gambar 2.11.
Gambar 2.11 – Ilustrasi operasi transformasi mixcolumns
|
 29
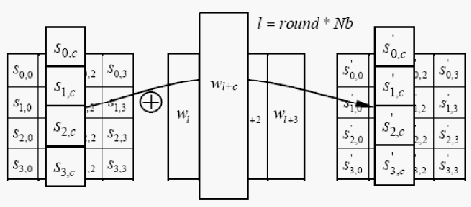
d. AddRoundKey transformation
Pada proses ini subkey digabungkan dengan state. Proses penggabungan
ini menggunakan operasi XOR untuk setiap byte dari roundkey dengan
byte yang bersangkutan dari state. Untuk setiap tahap, subkey didapatkan
dari kunci utama dengan menggunakan proses keyschedule. Setiap
subkey berukuran sama dengan state. Proses AddRoundKey ini dapat
dituliskan dengan persamaan berikut :
[S’0,c,S’1,c,S’2,c,S’3,c] = [S0,c,S1,c,S2,c,S3,c] [ Wround*Nb+c]
Untuk 0 = c < Nb ( c adalah kolom, dan Nb adalah jumlah blok ), pada
gambar 2.12 adalah ilustrasi transformasi AddRoundKey dengan
melakukan operasi XOR pada setiap kolom state dan kolom roundkey
yang didapatkan dari setiap round.
Gambar 2.12 – Ilustrasi transformasi AddRoundKey
Secara garis besar algoritma Rijndael memiliki tiga tahapan yang terdiri
keempat proses transformasi yang telah dibahas sebelumnya yaitu :
c. InitialRound
Pada round ini hanya dilakukan proses transformasi AddRoundKey.
|
|
30
d. Nr-1 Round
Pada round inidilakukan putaran sebanyak jumlah Nr-1 dan dilakukan
keempat proses transformasi secara berurutan yaitu SubBytes,
ShiftRows, MixColumns, dan AddRoundKey.
e. Final Round
Pada round ini dilakukan proses SubBytes, ShiftRows, dan
AddRoundKey.
2.5. Hash Function
Hashfunction merupakan sebuah algoritma yang mengubah text atau
message menjadi sederatan karakter acak yang me miliki jumlah karakter yang
tetap. Fungsi hash ini terkadang disebut juga a proveable collission resistant hash
function karena fungsi ini memecahkan beberapa masalah matematika yang sulit
seperti faktorisasi, log diskrit dan lain-lainnya (Contini, Lenstra, & Steinfeld,
2006).Hash juga termasuk salah satu bentuk teknik kriptografi dan dikategorikan
sebagai kriptografi tanpa key. Selain itu hash memiliki nama lain yang juga
dikenal luas yaitu “one-wayfunction”. Fungsi hash sendiri memiliki kegunaan
untuk menyimpan password, messageintegrity, dan messagefingerprint(Kaufman,
Perlman, & Speciner, 2002). Hash umumnya disajikan dalm bentuk bilangan
hexadecimal, yaitu kombinasi antara angka 0-9 dengan huruf a-f.
|
|
31
2.5.1. MD5
Algoritma MD5 dikembangkan oleh seorang Professor MIT yang bernama
Ronald L. Rivest. MD5 merupakan singkatan dari MessageDigestAlgorithm 5
yang sebelumnya dikembangkan dari MD2, MD3, MD4. Algoritma ini sedikit
lambat dari MD4 namun memiliki tingkat keamanan yang lebih baik. Algoritma
ini ditandai dengan empat tahap yang sedikit berbeda dengan desain MD4. Dalam
penggunaan MD5 tidak membutuhkkan biaya apapun untuk hak cipta, dan
algoritma MD5 ini sangat baik dalam hal teknikal (Xijin & Linxiu, 2012).
Algoritma ini selalu akan menghasilkan 128-bit ( 16 byte ) hash value.
2.6. Logaritma diskrit
Logaritma diskrit adalah sebuah permasalahan matematika dengan
persamaan sebagai berikut ax mod n = b, dimana a,n,b,x adalah bilangan positif
bulat dan n adalah bilangan prima(Shor, 1997).Perhitungan logaritma sampai saat
ini dipercaya masih sangat sulit untuk dipecahkan. Tidak ada solusi effisien pada
perhitungan di komputer untuk memecahkan masalah ini, sehingga logaritma
diskrit banyak dimanfaatkan untuk algoritma public-key cryptography. Jika kita
ingin menghitung ax mod n maka akan mudah mendapatkan nilai b, namun jika
kita lakukan operasi sebaliknya untuk mencari nilai eksponen ( x ) hal itu akan
lebih sulit dan membutuhkan waktu yang sangat lama. Berikut contoh
permasalahan logaritma diskrit :
f. 329 mod 17 = b
g. Maka b pasti bernilai diantara 0 – 16 , pada kasus ini jawabannya adalah
12.
|
|
32
h. Sebaliknya jika 3x mod 17 = 12, maka untuk mencari nilai eksponen x
akan lebih susah dibanding mencari nilai b.
Masalah logaritma diskrit sangat sulit diselesaikan terutama bila nilai n yang
berupa bilangan prima bernilai sangat besar(Witno, 2008). Beberapa solusi yang
digunakan untuk mencari nilai eksponen pada logaritma diskrit seperti Baby-giant
step, Function Field Sieve, Index Calculus Algorithm dan lain-lainnya. Beberapa
solusi tersebut masih kurang efektif karena tidak ada satupun algoritma solusi
yang berjalan
dalam hitungan waktu polynomial.
2.7. Aritmatika modular
Aritmatika modular merupakan sebuah sistem matematika untuk bilangan
bulat, dimana angka-angka dibungkus dalam suatu lingkaran terbatas setelah
mencapai nilai tertentu ( modulus ). Semua bilangan yang melintasi point yang
sama pada titik lingkaran adalah kongruen. Pendekatan modern untuk aritmatika
modular dikembangkan oleh Carl Friedrich Gauss dalam bukunya
“Disquisitiones Arithmeticae” yang diterbitkan pada tahun 1801. Aritmatika
modular banyak diimplementasikan pada metode kriptografi(Sihombing &
Gunawan, 2011). Aritmatika modular mirip aritmatika biasa, beberapa operasi
modular dapat difaktorkan sama seperti operasi matematika pada umumnya. Hal
ini sangat berguna terutama pada pembuktian kriptografi. Berikut beberapa sifat
dari aritmatika modular :
a. Identity
( a mod n ) modn = a mod n
nx mod n = 0 , untuk semua nilai positif bilangan bulat dari nilai x
|
|
33
b. Inverse
((-a mod n) + (a mod n) ) mod n = 0
c. Distributive
( a + b ) mod n = ( ( a mod n) + ( b mod n ) ) mod n
ab mod n = (( a mod n ) + ( b mod n )) mod n
d. Division
a / b mod n = ( ( a mod n) ( b-1 mod n) ) mod n
e. Inverse multiplication
( ( ab mod n ) ( b-1 mod n) ) mod n = a mod n
f. Exponentiation
ab mod c = ( (a mod c)b ) mod c
g. Multiplication
(a * b) mod c = (a mod c * b mod c) mod c
Pada kriptografi banyak yang menggunakan perhitungan aritmatika
modular, karena perhitungan logaritma diskrit merupakan persoalan yang sulit.
Aritmatika modular lebih mudah dikerjakan pada komputer, karena operasi ini
membatasi hasil yang didapatkan sehingga hasil operasi dari k-bit modulo n tidak
akan lebih dari n. Salah satu metode yang dapat digunakan untuk menghitung
operasi pemangkatan besar bilangan bulat modulo ( am mod n ) dengan cepat
adalah algoritma fast exponentiation (Schneier, 1996).
|