|
BAB2
LANDASAN TEORI
2.1
Das11.r-dasar Ge-IGmbang Suar.a---
---- ---- -
Secara sederhana suara yang didengar adalah
getaran dari suatu obyek
yang
merambat
di
udara kemudian sampai di telinga.
Sebelum dibahas
tentang bagaimana
pengclahan suara secara digital akan
lebih baik kalau dimengerti terlebih dahulu tentang
apa itu gelombang suara.
2.1.1
Definisi Suara
Secara fisis,
suara
dapat
diartikan
sebagai
penyimpangan
tekanan,
pergeseran
partikel dalam
medium elastik
seperti
udara. Pengertian
ini adalah
pengertian
suara
obyektif
Secara
fisiologis,
suara
adalah
sensasi
pendengaran
yang
yang disebabkan penyimpangan
fisis yang dijelaskan
dalam pengertian diatas. Ini
adalah suara
subyektifi
Dalam
penelitiatt
ini
suara
diasumsikan
sebagai settsasi
pettdengaratt
yattg
lewat telinga dan timbul karena penyimpangan tekanan
udara. Penyimpangan
ini
biasanya
disebabkan
oleh
beberapa
benda
yang
bergetar,
rnisalnya
dawai
gitar
yang
dipetik atau garpu tala yang dipukul sehingga mengeluarka,"l frekuensi tertentu.
Rambatan
gelombang
suara
disebabkan oleh
lapisan
perapatan
dan
perega.ttgan partikel-partikel
udara
yang
bergerak
ke
arah
luar,
yaitu
karetta
penyimpangan tekanan. Ini
sama
dengan
penyebaran
gelombang air pada
permukaan
dari suatu
kolam pada
satu
titik
dimana
batu
dijaiuhkan. Partikel-partikel
udara
yang
meneruskan
gelombang suara tidak
berubah
posisi normalnya; mereka
hanya bergetar
7
|
 ,,,
'
'
8
disekitar
posisi kesetirnbangnya,
yaitu
posisi pa.rt:kel bila
tidak
ada
gelombang
suara
. yang
ditemskan. Penyimpangan tekanan
ditembahkan
pada
tekanan
atmosfir
yang
kira·
kira tunak
(steady)
dan
ditangkap
oleh
telinga.
(Doe!le,
1972,
p
14)
2.1.2
Frekuensi,
Amp!itudo
JmrJah
pergeseran
atau
osilasi
yang
dilakukan
sebuah
partikel
dalam
1
detik
disebutfrekuensi.
Tiap
osilasi
yang
lengkap
disebut
satu
cycle.
Satuan
frekuensi
adalah
hertz
(Hz),
yang secara
numerik
sama
dengan
satu
c-ycle
per
detik
(cps-cycle per
second).
Suara
terendah
yang dapat
didengar
(audible)
oleh
telinga
manusia
mendekati
20
Hz,
yang
berarti
20
cyele
detik. Sebenarnya
suara yang
reru:lah
!ebih
dirasa.lcan sebagal
getaran
daripada
sebagai suara.
Suara
tertinggi yang dapat
didengar
terga.'"lt>J.'lg dari banyak: faktor
seperti
lingkungumur, dan
banyak
faktor,
tetapi
tidak
pemah
me!ebihi
20.000
Hz.
Lain hainya,
dengan anjing yang
dapat
mendengar
dari
40.000
Hz, kekelawar
bahkan
lebih
80.000
Hz.
Gambar
2.1
menjelaskan
frelk:uE,nsi dan amplitudo suatu gelon::bang.
;
;
'
'
.
'
1/\
II'
II'
"
t
•
l
w
\
I
i
;
]
6
t
t
\I
\J
\J
--
z
:If<
\}
\
t
&unbar 2.1Fre!meru;; dan
knpllmdo matu
GeEombamg Suara
|
 9
Satu
gerakan
penuh
gelombang suara
disebut
satu
cycle
(putaran)
yang
terdiri
dari
setengah putaran
pemampatan
molukel
udara
diikuti setengah
putaran
penjernihan
molekul
udara.
Jika
digambarkan
dalam
bentuk
grafik
atau
diubah
ke
dalam
bentuk
isyarat
listrik
dan
ditampilkan
pada
layar
osiloskop
maka
tinggi
gelombang
dari
puncak
atas
ke
bawah
disebut
amp!itudo.
Amplituda
menyatakan
I
menentukan
volume
(kuat
I
lemahnya)
suara.
W.lllkin besar
amplituda maka
suara
akan
terdengar
lebih
keras.
2.1.3
Oktaf
Setiap
kali
:frekuensi
suara
berlipat
dua,
maka
dapat
dikatakan
naik
satu
oktaf.
Dan
setiap
tarun
hingga
setengabnya,
turun
satu
oktaf
dan
seterusnya.
Jadi
interval
antara
100
dan
200
Hz
adalah
satu
oktaf,
dan
interval
antara 1.000
Hz
dan
2.000
juga
satu
oktaf
Jangkauan
pendengaran
manusia
normal
(kondisi
baik)
antara
20Hz sampai
20.000
Hz,
mencakup
tidak
!ebih
darl
10
oktaf
55 Hz
no
Hz
220Hz
440Hz
880Hz
I76o Hz
3520Hz
7040Hz
Suara
dan
representasi
isyarat
listriknya
pada
audio
mempllllyai
awal,
lama,
dan akhir;
keadaatmya
tergantung
wakru.
Seperti
ketika
sehuah
isyarat
melewati
bagian
pera!atan
audio,
yang
dapat
mendatangken
tunda
(delay).
Sepanjang
waktu
tunda
ini,
misalkan
sepersepuluh
detik,
sama
untuk
semua
komponen,
untuk
semua
representasi
eli
:frekuensi tinggi sebaik
frekuensi rendah,
hal
ini
tidak
menjadi persoalan. Namun,
jika
|
|
10
waktu
tunda
bervariasi
sesuai
dengan
frekuensi
isya.rat, maka
dikatakan
perbedaan
fasa
atau
fasa tunda.
2.1.5
Docibe!(oB)
Pada
pembicaraan
tentang
perangkat
audio
seperti:
penguat,
pengeras
suam
dan
sebagainya
mn
selalu
ditemukan
satuan
tegangan
(lV
=
1000
mV),
daya
(lW
=
JOOO
mW).
Untuk
menyatakan
beberapa
:!>..ubungan maka
dalam
dunia
audio
menggunakan
suatu
satuan perjanjian
yang
dinamakan
"decibel"
atau
"dB".
Decibel
sendiri
tidak seeara klmsus merupakan sejumlah tetap
tegangan atan
satuan
tekanan.
Lebih
merupakan
perjanjian
perhandingan
tekanan,
mirip
seperti
pada
tatabahasa
seperti
lipat
dua (double),
lipat
tiga (tripple),
setengah,
seperempat
dan
seterusnya
:U.5.1Decibel
(Tegangan) dan Decibel
(Daya)
Dalam
hubungannya
dB
dengan
tegangan
(Volt)
adalah
sebagai
berikut
:
dB
volt=
20
log (Vo : V;)
V
0
=
Tegangan Output
(Volt)
V;
=
Tegangan Input (Volt)
pers. 2.1
Setiap
sebuah
Voltase
Output
berlipat
dua
dari
voltase
input
malta
dapat
dikatakan
naik
6
dB.
Jw.a
metipat
dua
iagi
atau
me!ipat
empat,
dikatakan naik
6
dB
+
6
dB= 12
dB.
Dengan
pemikiran
yang sama- 6 dB berarti
setengar1, ·12 dB
berarti
seperempat.
Sedar.gkan
hubungan
dB
dengan
daya (Watt)
adalah
sebagai
berikut:
dB Voh =
10 log
(Po
:Pi)
Po=
Power Output
(Volt)
P, = Power
Inp<rt (Volt)
pers.
2.2
|
|
11
Jika
menggunakan
deeibel umuk
memba11dingkan
kuantitas daya,
terdapat
perbedaan
dengan
membandingkan decibel untuk kuantitas
tegangan. Untuk
daya
ouput
yang
me!ipat dua
dari
daya inputnya dikatakan naik 3 dB
dan
jika melipat
dua
lagi atau
melipat empat,
dikatakan naik
6
dB.
Sedangkan
-
3
dB
berarti setengah, -6 dB
berarti
seperempat. Ketika menyatakan ting.lcat watt, decibel sering disingkat
dBW.
2.2
Toorema
Sampling
<ian. Aliasing
Dalam mengkonversi
gelombang
suara menjadi
informasi
digital ak:an
dikenal
dengan istilah
pencuplikan (sampling).
Dan
yang menjadi persoalan penting dalam
proses
pencuplikan
itu, adalah berapa
banyak sample
yang
diambil tiap detiknya karena,
hal
tersebut
berpengaru.h pada kejemihan
suara
yang
dlbentuk kembali.
Pencuplikan
(sampling)
itu sendiri berarti pengambilan besaran tegangan
listrik
seca.ra periodik yang
kemudian diubah
menjadi
deretan-deretan
nilal
digital
menjadi satu rangk:aiarr informasi digitaL
Format yang paling banyak digunakan untuk merepresentasikan
sinya!suara
seeara
digital
adalah Pulse
Code
Modulation.
Pada
umumnya, sinyal suara
diubah
menjadi deretan l'llal (PCM) seperti di bawah inL
m
Sebagai contoh akan digunak:an
sinyal sinus yar,g sederbana. Seperti sebuah
gelombang yang dibangkitkan olehobyek
yang bergetar. Garis yang terbentang
di
tengah gambar 2-3 merepresentasikan
tekanan udara
yang
normaL Bagian
gelombang balk kurv-a sebe!ah atas maupun
k"U!Va
di bawah
garis tengah tersebut
merepresentasikan perubahan tekanan
udara baik secara positif maupun negatif.
|
 12
\
1\
I
'\
'\
I
\
.I
\/
\J
\
\
·-
<
Time-
•
Berikutnya
sebuah
microphone
diguna.kan
untuk
mengkonversi
geiombang suara
(di
udara)
menjadi sinyal-sinyal
!i!l'..rik.
Besar
tegangan yang
dihasilkan
oleh
microphone
berkisar
±1 volt
seperti dalam
gambar
2-4.
+i.O
+0.5
0
-0.5
I
_J.
-1.0
Time
------·---)»
Grunbar 2.4
Sinyal Listrik
Tegangan
sinyallistrik
analog
dikonversikan
menjadi
sedereta.tl
nilai
o!eh
sebuah
perar1gkat
ya.ng
biasa
disebut
analog-to-digital converter.
Gambar
2.5
dibawah
ini menga\'11barkan
hasil
pengkonversi
16
bit
dari
analog
ke
digital
yang
mempunyai
keluaran
integers
dari
-32.768 ke
+32.767.
|
 I
f
1\
f\
\
\
\J
\
I
·\
'
Gambar 2.5 Analog-to-Digital Convene.-
Output
+32,767
+16,383
0
-16,384
-32,768
•
Karena
nilai tak
terhingga
dari
data
masukan
tidak
dapat
direkam
dan
dimhah
menjadi bentuk karakter dari sinyal,
maka contoh atau
sample
pada gambar
2.6
dibawah
ini
mengambil
intervai
yang
biasa
digunakan. Nilai
dari
oontoh
atau
sample
yang diambil setiap
deti.k
dinamakan
sampling rate.
Pada gambar
2.6
dibawah ini dapat dilihat 43 sampies yang
telah
diambil.
1
43
+32,767
+16,383
0
-16,384
-32,768
Gambu 2.6 Cupliklm
s!uya!yang
diam!Jil
•
Hasil
dari ke
43
samples
mewakili
posisi
gelombang
pada
setiap
intervalnya
ditunjuka.1. pada gambar 2.7 dibawah ini.
|
 14
-
:--T
rd
ed
Va
lue
,
43
+32,767
+16,383
0
-16,384
-32,768
Komputer kemudian
dapat membangun
ulang gelombang sinyal dengan
menghubungkan titik-titik cuplikan
data
yang
didapat.
Basil dari gelombang
sinyal yang telah dihubungkan dapat dil!hat
pada
ga.t-nbar 2.8 seperti dibawah
iili.
:
II
+32,767
+16,383
rd
ed
I
Va
Ill
iu
i
-+-
43
0
-16,384
-32,768
Dapat
disimpulkan bahwa
teijadi
perbedaan
antara
samples
yang
asli
dengan
hasil dari
pembentukan
ulang :
a. Ni!ai yang
dibangkitkan
o!eh
analog-to-digital
converter
ada!ah
nilai
integers
b.
Keaku:ratan
hasil
bentuk
gelombang
tergantung
dari
banyaknya nilai
dari
samples
yang
diambil.
|
|
14
|
|
15
Pada
umumnya
t>.:mya nilai angka
yang
terbatas
yang dapat
ditampilkan
pada
ge!ambang
analog
dengan
keakuratan
yang
terbatas.
Hal
yang
penting
yang
hams
diingat
bahwa
kebanyakan
perangkat
keras
audio
tidak
memproduksi
gelombang
dengan
eara
pengirirnan titik-titik
data
seeara
linier.
(seperti
dalam
gambar
2.8).
Karakteristik
electron.ik
dari
peralatan
digit£4/-to-analog
converter adalah
perangkat
yang
mengubah
atau
mengkonversi
titik-titik
data ke
persamaan
level
tegangaP.,
dan
pada
unmmnya
dihasilkan
ge!ombang
dengan
bentuk
kurva
yang
cukup
halus.
Dalam
melakc..J.kan
pencuplikan
(sampling) sehlngga
dihasilkan
suara
yang
jernih
maka.,
frek-uensi
pencuplikan
(sampling)
hams
dua
kali
atau
lebih
dari
frekuensi
terbcsar
sinyal
yang
akan disampling.
Hal
ini
diindikasika11
dalam Nyquist
sampling
theorem
bahwa
suatu
sinyal
analog
dapat
disamp!ing
dertgart
balk
bi!a
frekuensinya
(h)
tidak
lebih
dari
setengah
frekuensi
sampling
if,).
Pemyataan
ini
dapat dituliskan
da!am
persamaan
matematika
sebagai
berilrut :
/a
::;;
0.5/s
pers. 2.3
Untuk
frekuensi
sampling
yang
kurang
dari
dua
kali
frekuen.si
aslinya
maka
yang
te!jadi
adalah
sinyal
baru
(yang
terbentuk
dari
sample-sample
yang
diberikan)
yang
tidak
sama
dengan.
sinyai
aslinya
(Currington,
1995).
Hal
ini
mengakibatkan
infurmasi
yang
terkandung
dalam
sinya! analog
tidak
lengkap sehlngga
mengaburkan
sinyal
aslicya.
Tenentuknya
sinyal
bam ini
dinamakan
efek
Aliasing.
Efek
aliaSing
ini
dapat
dihindari
dengan
menerapkan
teorema
Nyquist
tersebut
(pers.
2.3).
|
|
|
 16
3
2
"
a
"
'
j
d.
Analog frequen y"' 0.95 of sampling
rate
I
·
""
0
<
-I
·
\
•
Time
(fir
Silmple number)
Pada
gambar
2.9
memperlihatkan
frekuensi
yang
terbentuk
dari
efek
aliasing.
Dari
gambar
2.9
di
atas
terlihat
bahwa
frekuensi
sinyal
analog
lebih
besar
dari
setengah
frekuensi
sampling.
Sample
yang
didapat
berupa
kotak
kecil
berwama
hitam
membenruk
sinyal
analog
baru
yang
tidak
sernpa
dengan
sinyal
analog
aslinya,
dalam
hal
ini
adalah
frekuensi
sinyal
analog
yang
baru
memi!i!d
frekuensi
diantara
frekuensi
terendah
sampai
dengan
frekuensi
tertinggi
sinyal analog aslinya.
Efek
aliasing
dapat dilihat
langsung
pada
domain
waktu
seperti
ga,'!lbar 2.9,
juga
dapat
dilihat
pada
domain
frekuensL
Pada
domain
frekuensi,
efek
aliasing
diperlihatkan
dengan
speklrum yang
tw11pang
tindih
seperti
terlihat
pada
gambar
2.10.
-3-j------,,---,----,----,---:
G
Gambar :Z.ln Efek
P.Jiasing
lliltom dnmain frekuensi (frekuensi domain)
|
|
17
2.3 Fast Fimrier Transform
(FFT)
Transformasi
Fourier
mengkonversi
informasi dalam
domain
wak:tu
kedalam
domain
frelruensi.
Hal tersebut
amatlah
penting
dalam
penganalisaan dalam
bidang
antara
lain
telekomunikas
speech,
pemrosesan
sinyal
dan
pemrosesan
citra.
Dalam
sistem
wak:tu
diskrit,
transformasi
fourier yang dipakai
adalah
DFT
(Diskrit Fourier
Transfonn).
Dikarenakan
DFT
dalam
proses
perhitungannya
amatiah
rumit, maka
sangat
sedikit
aplikasi
yang
mengimplernentasikan
DFT, bahkan
dalam
komputer-komputer
modem
metoda
DFT
ini
jara.'1g
digunakan.
Fa:.t
Fourier
Tran:sform
(FFT)
mempakan
algoritma
yang
efisien
untuk
mengimp!ementasikan
DFT
dan
a!goritma
ini
amat
banyak
digunakan
dalam
berbagai
area
pemrosesan
sinyal
digital.
Tetapi
untuk
dapat
memahami
bagaimana
menggunakan
FFT
dalam
aplikasi
yang
ada terlebih
dahulu
hams
dimengerti
apa
itu
DFT
dan
bagaimana
mengimp!ementasikannya.
:z.::U
Discrete Fourier
Trantiform
(:0
FT)
2.:U.l
Format
dan Notasi Real DFT
Seperti
terlihat
pada
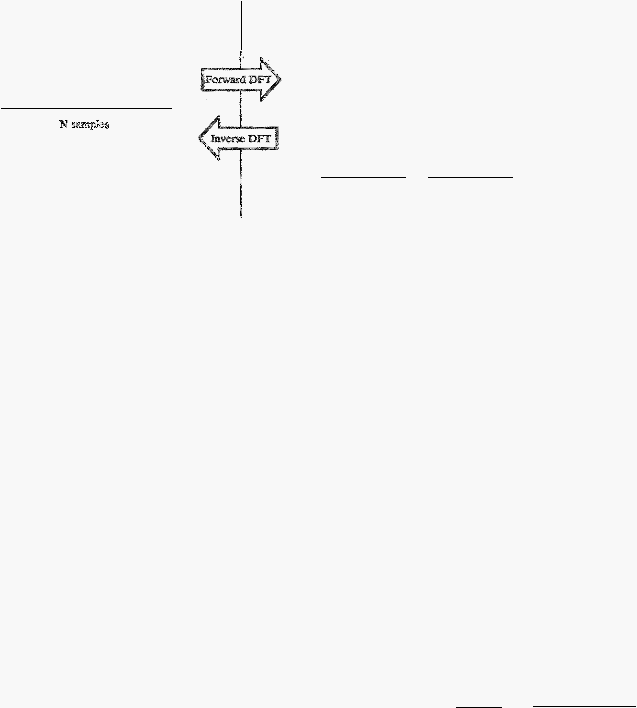
gambar
2.11,
Discrete
Fourier Transform
(DFT)
merubah
input
N-point
menjadi
dua sinyal output
N/2
+
1
point. Sinyal
input
biasa
disebut berada
dalam
domain waktu
(time domain),
karena
biasanya
sinyal
yang
memasuki
DFT
disusun
dari
cupli..kan-cuplikan
(sample-sample}
berdasarkan
interval
waktu
tertentu.
Sedangkan
istilah
domain
frekuensi
(frequency domain)
digunakan
untuk
menggambarkan
amplituda da.-i gelomb!nlg sinus
dan
kosinus
yang
merupakan pecahan
dad
sinyal
input
pada
DFT.
|
 18
Domain
frekuensi
dan
domain
wak:tu pada
dasarnya
mengandung
inforrnasi
_ yang
sama,
hanya
saja
bentuknya
berbeda.
Jika
diketahui
salah
satunya
maka
yang
lainnya
dapat
dihitung.
Jika
diketahui
domain waktu
dari suatu
sinyal, proses
perhitungan
untuk
menjadikan
domain
frekuensi
disebut
dekomposisi,
analisis,forward
DFT
atau
biasa
disebut
DFT.
Jika
diketahui
domain frekuensi,
proses
perhitungannya
disebut dengan
sintesis
atau inverse
DFT
Time
Domain
Frequency Domain
x[
]
ReX[
I
lmX[
J
Liltlt!ltl
rrtlllliib
0
Nil
()
N/2
NJl+l
es
Ni2+1
SiiJUp-1cs
(cQril:e
hm't'
mftfr!ir.rtk.t)
Mm:
;ml't:'
WJPiillll.!e,,-J
collective!y referred
tc
as
xt
l
Gamba2.11 Fermat
dan
New!dar!
Red
DFI'
Ba.."lyaknya
cup!ikan
dalarn
domain
waktu
biasa
direpresentasikan
dengan
variabe1
N,
dimana
N
adalah
bilangan
integer
positif
dan
biasanya
kuadrat
dari
dua
(2")
seperti
128,
256,
512,
l024,
dan
seterusnya.
Ada
dua
hal
yang menjadi
latar
belakang
kenapa
digwnakan
kuadrat
dari dua
ya.'tu :
•
Penyimpanan data
digital
dilakukan
secara
pengaiamatan
binary (binary
addressing).
"
Algoritma
yang
sangat
efisien
untuk
menghitung
DFT
yaitu
FFT (Fast
Fourier
Transform)
biasanya
dioperasikan dengan
N, dimana
N
adalah
kuadrat
dari dua
(2n)_
Pada
banyak
kasus,
cuplikan
diambil mulai
dari
0
sampai
N
-
l bukan
dimulai
dari 1
sampaiN.
|
|
19
|
|
20
Pada
notasi
standar DSi'
(Digital
Signal
Processing),
untuk
merepresentasikan
sinyal
dalam
domain
waktu
digunakan
burufkecil
seperti
x[],y[],
dan
z[],
sedangkan
untuk sinyal
dalam
domain
frekuensi
direpresentasikan
dengan
huruf
besar seperti
X[], Y[],
dan
ZO
Jika
terdapat
sinyal
input
dalam
domain
waktu
yaitu
x[]
sebanyak
N-point
Maim
domain
frekuensi
untuk
sinyal
ini
adalah
X[]
yang
terdiri
dari
dua
bagian
dimana
masing-masing
bagian
merupakan
array
dari
cup!ikan
sebanyak
N/2
+
l. Bagian
pertama
disebut
dengan
bagian
real
dari
X[]
dan
biasa
ditu!is
dengan ReX[],
sedangkan
bagian
kedua
disebut
deng&'l bagi&'l
imajiner
dari
X[]
da.'l
biasa
ditulis
dengan
ImX[l.
Nilai
dalam
ReX[]
adalah
nilai
amplituda
dari
getombang
kosinus,
sedangkan
ImX[]
berisi
nilai amplituda
dari
gelombang
sinus.
2.3.1.2
Fungsi
Dasa!!" dari
DFT
Gelombang
sinus
dan
kosinus
yang
digunakan dalam
DFT
umumnya
disebut
dengan
fungsi
dasar
DFT
(DFT basic fimction).
Dengan
kata
lain
keluaran DFT
adalah
sebuah
himpunan nilai-nilai
yang
merepresentasikan amplitudo-amplitudo.
Jika
diberikan
nilai
amplituda
(pada
domain
frekuensi)
ke
gelombang
sinus
dan
kcsinus (yang merupakan f,mgsi
dasar) secara
tepat hasilnya
adalah
sebuah
himpunan
gelombang
sinus
dan
kosinus
yang
ter-ska!a
dimana,
bila
dijumlahkan
antam
keduanya akan
menghasi!kan
bentuk sinyal
dalarn
domain
wak:tu. Fungsi
dasar DFT
dibangkitkan
dari persamaan
berikut
:
c.
[l']c
cos(2rr:ki
IN)
s
.[i]"'
sin(
2rr:ki IN)
pers. 2.4
|
 20
dimana
ck[J
adalah
gelombang
kosinus
yang
nilai
amplitudonya
berada
dalam
ReX[k],
dan
sk[]
adalah
gelombang
sinus
yang
nilai amplitudonya
berada
dalam
ImX[kJ_
k
sei1diri merupakan
parameter frekuensi yang
menunjukkan
berapa
sik!us
yang
te!jadi
untuk
menyelesaikan
N-point
dari
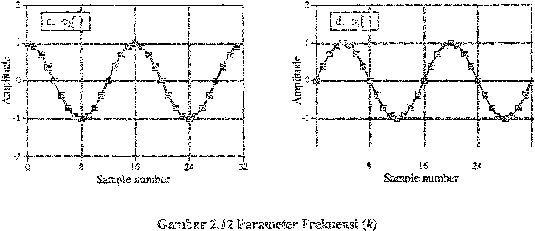
sinyal. Untuk
lebih
jelas
perbatikan
gambar
2_12_
c2fJ
adalah
gel.ombang kosinus
yar.g
membuat
dua
siklus untuk
menyelesaikan N-point
dari
sinyat
-1+---li----+--+----1
2.3.1.3
Analisis, Menghitung
Forw(Ud
DFT
Perhitungan
DFT
dapat
diselesaikan
dengan tiga
cara
yaitu
;
simultaneous
equations,
korelasi
dan
terakhir
dengan
FFT
(Fast Fourier Tran.ifonn)_
Pada
tugas
skripsi
ini
hanya
akan
dibahas
algoritma
FFT
untuk
menyelesaikan
DFT_
Lebih
lengkap
tentang
algoritma. FFT
ini dapat
dilihat
pada bagian
2.3.4 _
2.:3.1.3.1
li''<erhitungan DFT
untuk Deret
Real2N-
Titik
Algoritma DFT dirancang
untuk
melakukan
perka!ian
dan
penambahan
kompleks
walaupun
inputnya
mungkin
bemiial
rea!.
Alasan
dasar
untuk
situasi
ini
adalah
karena
faktor-faktor fasenya
(WN)
kompleks.
Perhitungan
yang
lebih
efisien
bisa
|
|
21
l
didapatkar.. dengan
membentuk deret
bernilai-kompleks
dari
deret
bernilai-real
sebelum
.
dihitung
oleh
DFT.
Dengan demikian, hanya
diper!ukan satu DFT N-titik
untuk
menghitung
deret
bernilai-real
dengan
2N-titik.
Anggap
input
DFT
adalah
g(n)
yang
merupakan
deret
bemilai-real
dengan
2N-titik.
Deret
g(.'1)
dipecahkan
menjadi
dua
deret
(berindeks
genap
dan
berindeks
ganji!), yair.x
x,.(n)= g(2n)
pers.
2.5
dar.
X1
(n)= g(2n+
1)
pers.
2.6
dengan
n=O,I,...,N
L
Dua
deret
ini
digabungkan
(di-packing)
menjadi
satu
deret
kompleks,
yaitu:
x{n)=x,(n)+ jx
2
(n)
n=O,l,...,N
-1
pers.
2.7
Sifat
operasi
DFT
ada!ah
iinier
dan
karena
itu DFT
dati
x(n)
dapat
dinyatak:an sebagai:
X(k)=X,(k)+ jX
2
(k)
k=O,I,...,N-1
pers.
2.8
Deret
x1(n)
dan
x2(n)
da;;at dinyatakan
dari
segi
x(n},
sebagai
berikut:
x;(n)
x(n)+x"(n)
2
pers.
2.9
1
)-
x(n)-x*(n)
X,l(l -
2j
pers.
2.10
Sehingga
DFT
dari
XJ(n) danxJ(n)
adalah
X
1
(k)={DFT[x(n)]+DFT{x*(n))}
pers.
2.11
X
2
(k)= Zj
{DFT[x(n)j-DFT[x*(n)]}
pers.
2.12
|
 22
DJ<T dari x*(n) adalahX*(N-k), oleh
karena
itu
XJ{k) danX 2(k)
dapat
ditulis:
x,(k).!.[x(k)+ X*(N k)]
2
pers.
2.13
x,(k)=-f:[x(k)-- X*(N
-k)]
"-}
Pers.
2.14
Deret
berindeks
genap
XJ(k) menjadi
komponen
real sedangkan
deret
berindeks
ganjil
X2(k)
rnenjadi
komponen imajiner pada
deret kompleks
yang
menjadi
input
untuk
DFT
2-titik
pada unpacking.
DFT
2N-titik
dari
g(n)
bisa
dinyatakan
dari
segi
kedua
DFT
N-titik
X1(k)
dan
X2(k). Untukmembentuk (unpacking}
G(k)
d&-iXJ(k)
danX?(k},
dila.lrukan:
pers.
2.15
N-!
N-1
G(k)=
L;x,(n)W;' +W,',L;x,(n)W:;'
pers.
2.16
Sehingga
dengan
memanfaatka.'l sifat
simetri
dan
keperiodikan faktor
fase Wl-1
,
pers.
2.17
pers.
2.18
G(N -1)
G(N)
G(:ZN-1)
Gambar 2.13
Unpawld11g
|
|
|
|
23
=- -
:t3.1A Sintesis,Menghit11ng inverse
DFT
Persarnaan
sintesis
(untuk
menghitung
inverse
DFT/ IDF1)
dapat
ditulis
sebagai
berikut
:
N!1
N/1
x
]=
:Z::ReX[k]oos(2rt.ki/N)+ _l)mX[k]sm(2rt.ki/N)
pez;s. 2.19
Persamaan
di
atas
menggambarkan
bahwa
sinyal
N-point,
x[i], dapat
dibuat
dengan
penjumlahan
N/2
+
1
ge!ombang
sinus
dan N/2
+
1
gelombang
kosinus. Persamaan
sintesis ini
hakikatnya adalah
menga!ikan amplituda
(ya.;1g terletak
dalam
IrnX!k]
dan
ReX[k])
dengan
fungsi
dasar
(sm(27dd/J.l)
dan
oos(27dd/N))
untuk
membuat
sekumpulan
gelornba11g
sinus
dan
kosi!lUs ter-skala.
Penambahan
keduanya
(gelombang
sinus
dan
kosinus
yang ter-skala)) menghasilkan
sinyal
dalam
domain
V.'liktu, x[i].
Pada
pers.
2.20,
terlihat
ReXlk]danlmX[k] bukannya ReX[k]
dan
IrnX[kJ.
Hal ini.
dikarenakan amplituda
yang dibutuh.lrn.n
untuk
operasi
sintesis
berbeda
dengan
domain
frekuensi
dari
sinyal.
Walaupun
demikian
tidak
sulit
untuk
melakukan
konversi,
hanya
dipedukan normalisasi
sederhana,
seperti
berikut
:
-r
1
Rexrk]
ReXLkJ=---- •
N/2
·
Im
-
Xe
1c
,]
ImX[k]
N/2
pers. 2.20
keeuali
untuk
dua
kasus
khusus
yaltu
ReX[OJ
=
ReX[O]
N
ReXJ:N /2]
=
ReX[N /2]
N
pers. 2.21
|
 .
•
i
24
Jadi, terdapat dua iangkah untuk mencari hubungan domain
waktu
dari domain frekuensi
yaitu:
"'
Keta. ui
terlebih
dahulu
amplituda
dari
gelombang
kosinus
dan
smus
(
Re
X[kJ
dan Im
X[k])
@
Se!anjutnya,
hltung
ReX[k
]dan
Im
X[k]
nya
dengan
rumus
konversi
pada
pers.
2.20
atau
pers.
2.21 (hila
termasuk
ke dalam kasus khusus}
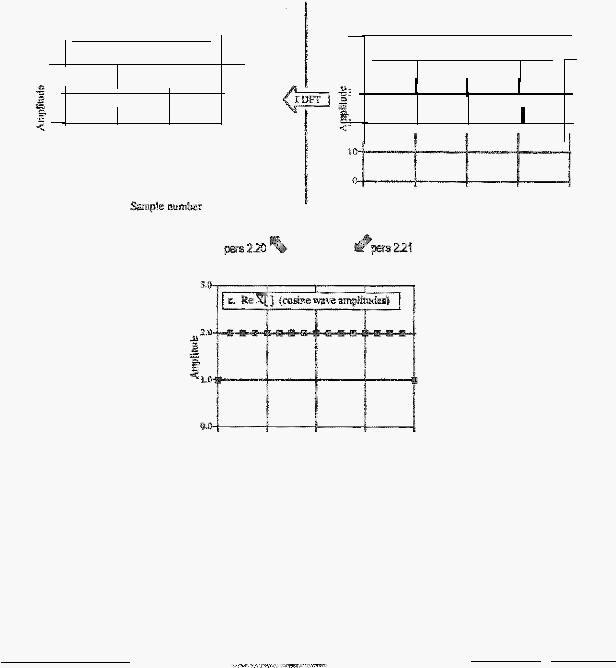
Perh<tikan gambar 2.14 berikut
,
Time Domain
.
' I
a.
!h
tlm;,domain s! ;no!
j
i
Frequency Demain
I!>.
bX[] (mellequencyd
molnl
I
•o
_i
!
;;Q
'
l
I
'
31}
l"
I
I
'
0
I
S
ll
!6
l'mqru>tl>cy s;nr.p!mmber
,;
s
12'
!6
F'r uJncy
sa.-np!e ID:;.'Tibe
Gan:!IYar 2.14lnverse DFT
|
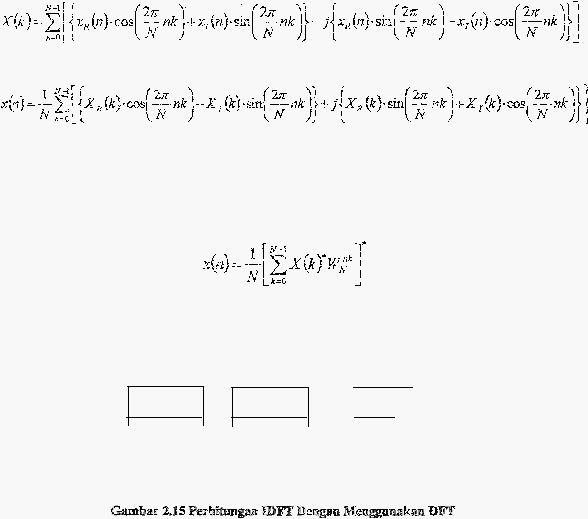 25
1
2.3.1.4.1 Menghitamg IDFT Dengan
Menggunakan DFT
Rumus
analisis
dan
sintesis
DFT
didefinisikan:
N-1
_2-,r
k
X(k)= :
·
Lx(n)e-
"N"
no-=G,l,...,N
-l
pers.
2.22
1
N-1
-
.1rt
fr
x(n)=-:LX(k)/'N"
n
= O,l,...,N -1
N,""
pers.
2.23
Bi!a
rumus
diatas
dipecahkan
menjadi
komponen
real
dan
imajiner,
malca
X(k) dan x(n) menjadi:
Dilihat
dari
penurunan
rumus diatas,
mFT dari suatu
deret
bisa
divitung
dengan
menggunaka.ll
algoritma DFT,
yaitu:
pers.
2.24
dimana
notasi
'*'
menunjukkan akar
sekawan
(konjugasi kompleks). Rumus
diatas bisa
digambarkan:
I
I
f---x(n)
X(k)
11*
'--
OFT
[!*
I
'
N
|
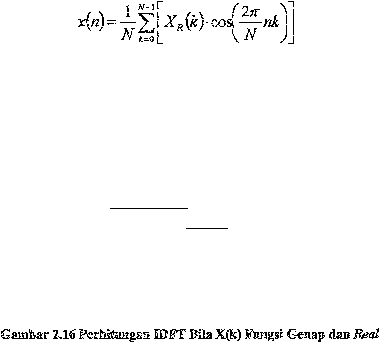 26
Jika
X(k)
adalah
deret
pemilai-reai (X(k)'
=
X(k)) dan X(k) ada!ah
fungsi
genap (X(k}
=
X(-k))
rnaka
DFT
dari
X(k)
beroJlai real
sehingga
tidak
ada
operasi
konjugasi
kompleks
yang di!akukar:
pers.
2
25
Bila
menggunakan
algoritma
DFT, Pers. 224
untuk
X(k)
yang
merupakan
fungsi
genap
dan
bernilai-real bisa disederhanakan
menjadi:
l
N·l
x(n)=-:LX(k)w;•
N,
X(l<)
DFT
1--X(n)
1
N
2.3.2
Sifat-Sifat
DFT
Sifat-sifat
dari
Transforw.asi
Fourier
Diskrit
antara
lain:
pers.
2.26
2.:3.2.1
Periodik
ftka
x(n)
dan
X(k) adalah
suatu
pasangan DFT
N-titik
dengan
0,;;,
n
s
N
-1
dan
OsksN-l,maka·
x(n+N) =x(n)
untuk
seluruh
n
pers. 2.27
X(k+N)= X(k) untukseluruh k
pers. 2.28
Sifat
keperiodikan
ini
mengikuti
sifat
keperiodikan
dari
eksponensial
kompleks.
|
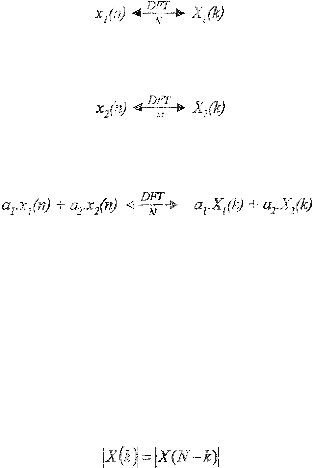 27
·COSJ
)
2.3.2.2
Une.mritas
Jika
dan
kemudia11 untuk
setiap
konstanta
a1 dan
a
2
bernilai
real atau bemilai
kompleks,
maka
:
pers. 2.29
2.3.2.3
Sifat Simetri DFT
dari
Barisan Bemilai Real
Jika
deret
x(n) real, ( x
1
(n)
=
0
),
maka
x(f;)= x·(N -k)
pers. 2.30
atau
pers. 2.31
LX(k)=-L.X(N-k)
pers.
2.32
DFT
dari
deret
real
menghasi!kan
deret
frekuensi
real
yang
merupakan deret
genap
dan-
deret frekuensi
imajiner
yang
merupakan
deret
ganjil.
Jika
x(n)
deret
yang
bernilai
real
dan
genap,
yakn
x(n)= x(N -n)
maka
DFT
dari
x(n)
akan
menghasilkall
X,(k
)=
0
sehingga
DFT
menjadi
1
)
x()
(2·'ff·k·n\
X
._k
=
;t_,
n
"""
\.
N
pers.
2.33
|
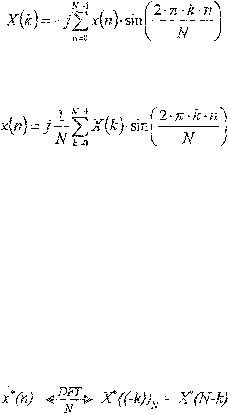 28
yang
bernilai
real
dan
genap. Karena
XAk)=
0, IDFT
merJadi
X:
{
-(1
'J
=-,
1
t...
X
.
(k)
·C
f2·7!:·k
-
·n\)
pers. 2.34
Nk=O
N
Jika
x(n)
deret
yang
bemilai
real
dan ganJil,
yakni,
x(n)=-x(N-n)
makaDFT
dari
x:(n)
a.l;:an
menghasilkan
XAk)"'
0
sehinggaDFT
menjadi
yang
bernilai
imajiner
dan
ganjil.
Karena
X
11
(k)=
0, IDFT
menjadi
2.3.2.4
Sifat Konjngasi
Kompleks
Jika
x(n)
·
_..
X(k)
maka
pers_
2.35
pers.
2.36
pers.
2.37
|
 29
2.3.2.5
Pembalikan
Wakru Suatu Barisan
Jika
x(n)
<
DX: (k)
maka
x((-n))N
c
x(N-n)
<!
DFT
"'
X((-k)N
=
X(N-k)
pers.
2.38
2.3.2.6
Konvolusi Melingkar
Jika
dan
maka konvolusi melingkar dari deret x
1
(n) dan x
2
(n):
pers. 2.39
2.3.2.7
Perkalian
Dua Barisan
Jike
dar1
|
 30
2
.
N
N
N
-
N
maka
pers.
2.4D
1\.fasalah yang
dih.adapi
dalam
menjala11kan
DFT
adalah
dalam
menghltung
sederetan
N
buah bi!angan
kompleks
hk
(pers.
2.41)
untuk
mengbasilkan deret
Hn
(pers.
2.42)
yang
berisi
N
buah
bilangan
kompleks.
Dapat
dilihat
bahwa
untuk
setiap
harga
k,
DFT
akan
melakukan
N
buah
perkalian
bilangan
kompleks
(
4N buah
bilangan
perkaiian
real)
dan
N-l buah
penjumlahan
bilangan
kompleks
(4]\l-2 buah
penjumlahan
bi!angan
real).
Sehingga
untuk
menghitung
keseluruhan
N
buah
data,
akan
diperlukan
!.f buah
perkalian
kompleks
dan
N2
-N
buah
penjumlaha.'l kompleks. Perhitungan DFT
ini
sangat
tidak
efisien,
karena
tidak
memanfaatkan sifat
simetrik
(pers.
2.43)
dan
periodik
(pers.
2.44)
dari faktor
phasa
W;v
=l-
%
.
h,
""h(kli),
dnnana n
=
--,...,--
2
2
Sifat
simetrik:
W
n+N/,.
-
-W"
pers.
2.41
pers.
2.42
pers.
2.43
Sifat
Periodik:
pers. 2.44
Aigoritma
yang
memanfaatkan
kedua
sifat
ini
dikenal
dengan
nama
Aigoritma
Fast
Fourier
Transfonn.
|
|
3!
e
'
pers.
2.46
2.3.4
Fast Four'.er Transform
(FFT)
2.3.4.1
FFT dengan
algoritma Radix-2
Secant mendasar,
kesulitan
DFT
ada!ah
perhitungan terhadap
sederetan
X(k)
yang
bernilai
kompleks
yang
dihasi!kan
dari
sederetan
x(n)
yang
juga
bernilai
kompleks
seperti
ter!ihat
pada persamaan
DFT
berikut
:
N t
X(k)=
l:,x(n)·e-F"''"'•kfN
OsksN-1
"""
pers.
2.45
Untuk
menyederhanakan
penulisan
persamaan
DFT
di
atas,
biasanya
didefinisikan
faktor
phasa
WN
yar,g berniiai
kompleks
dimana
:
TTT
-j2·n·n-J:!N
rrN--
Schingga
pers.
2.45
dapat
dituiis
kembali
menjadi
:
N-1
X(k)=
l:,x(n)·w;·•
"""
pers.
2.47
Sebagai
konsekuensi
dad
persamaan
di
atas,
hila
dilakukan
perhitungan
untuk
setiap
nilai
X(k)
(sebanyak
N
kaii)
secara
langsung
maka.
dibutuhkan
perkalian
kompleks
sebanyak
N² dan
penjumlahan
kompleks
sebanyak
t.f
-N.
Perhitungan
secant
langsung
seperti
ini
tidaklah
efisien
karena
tidak
memanfaatkan
sifat
simetri
dan
sifat
periodik:
dari
DFT.
Perl:-titungan
DFT
yang
memanfaatkan
kedua
sifat
tersebut
secara
kolektif
di.nrunakan
FFT.
Salah
satu
algoritma
untuk
komputasi
FFT
yang
memanfu.atkan kedua
sifat
i.Pj adalah
algoritma
FFT
radix-2.
Dalam
skripsi
ini
digunakan
algoritma
FFT
radix-2
tersebut.
Algorit1na FFT radix-2
dikembangkan
dengan
pendekatan
devide-and-conquer,
suatu
pendekatan
yang
banyak
digunakan
dalam
perhitungan-perhituP.gan
pemrosesan
|
 3
X(O)
X(L}
...
I
j
I
X(l)
'
XrL+l)
!
".
X((M·l}{L+l))
I
...
'
;
X(L-1)
l
...
X(LM-1)
]
I
I
sinyal
digital.
Pendekatan
devide-and-conquer
ini
memecah DFT
N-titik
ke
dalam
beberapa
DFT
yang
lebih
kecil
untuk
diselesaikan.
Input dan
output
DFT biasa
disirnpan
da!am
suatu array dua dimensdimana
da!am penempatan
input atau
outputnya
bisa
berorientasi
kolom
(column-wise) atau
berorientasi
baris (row-wise).
Bila
terdapat
N-titik
dengan
N
adalah
bilangan
integer
yang dapat
difaktorkan
menjadi
L
dan M atau
dapat
ditulis
sebagai
berikut
:
N
LM
Ma.l{a indeks
yang
menunjuk
input
atau
output
ditulis
dengan
n,
indeks
yang
menunjuk
kolom (misalkan saja)
l
dan indeks yang menunjuk baris
m.
mak:a array yang
dapat
dibentuk
sebagai
berikut
:
m
=
indeks baris
0
l
a
0
.9
l
...
M-1
X((. ·l)L)
I
I
.ri
-
II
L-1
Xf2f.-ll
Gll!mbar 2.17
Array
Dua
Dimens!Berorienwi Kolom (Column-WKSe)
m
=
mdeks baris
0
l
]
I
I
...
!
M
-
i
-i
.
"0
s
ll
()
L-1
X(O)
}{(M)
.I
i
I
'
J
X((L-l)M)
'
X(l)
X(M+l)
i
I
...
X(M-1)
...
X(2M-1)
i
...
I
I
X((L-l)M+l) I
...
X(L -l}
Gambar :2.18 Array Dua
mme11si
Berorientasi Baris (Row-Wise)
Dengan
demikian, pendekatan
devide-and-conquer
ini
dapat dipakai
bila
N
bukan
bilangan
prima_
Algoritma
FFT
radix-2 adalah
perhitungan
terhadap
DFT
N-titik
dimana N
=
r• ,
r
adalah
bilangan
radix
dan
dalam algoritma
ini
bemilai 2. Dengan
|
 10
8
33
penjelasan
sebelumnya
bahwa
input
dan
oui:put
disimpan
dalam
array
dua
dimensi
maka
dapat dibayangkan
bahwa
array
yang
terbentuk
akan
memiliki
2
baris
dan
N/2
kolom
atau
merniliki
2
kolom
dan
N/2
baris,
sebingga
seo!ah-olah
akan teljadi
pemisahan
antara
titik
ganjil
dan
titik
genap.
Sebagai
ilustrasi,
hila
terdapat
sinyal
dengan
16
titik
dan
akan
dihitung
dengan
aigoritrna
FFT
radix-2
ini maka
sinyal
16
titik
tadi
akan
dipecah
menjadi
bagia.n-bagian
yang
kecil
(bagian penyusunnya)
dan akan dipisabkan
antara
penyusun
garljil dan genap
seperti
terlihat
pada
gambar
berikut
:
1
sinyal16 tilik
o
1
2
a
4
s
a
7
a
9
10 11
12
13
14
1s
1sl yal8mlk
ro
2
.:
s
a
10
12
14
11
1
3
s
1
s 11
1s 15
Jl
Jl
1
sir.yal41i'jk
o
4
a
12
ji 2
e
10 14
II
1
5
9
13
j!
3
7 11
15
I
1sinyal2tilik
Jl
¥'
Jl
Jl
2
,(\tJI\t,( ,(
,(
JI
,(
Ji\t
1
sinyal1tilik
[!J @J0EJ0EJ 00EJ[J[22][2JEJ
Pada gambar
di
atas
terlihat
bahwa
susunan
bit
inputnya
mengalami
perubahan
seteiah
dilakukan
pemisahan
terhadap
penyasun
ganjil
dan
genap.
Perubahan
yang
terjadi
mengikuti
poia
tertent"<.l, dirnana
bit
paling
kiri
(MSB)
di
pindahkan
·menjadi
bit
pa!L11g kanan
(LSB).
Untuk
lebih
jelas
perhatikan
ta:bel
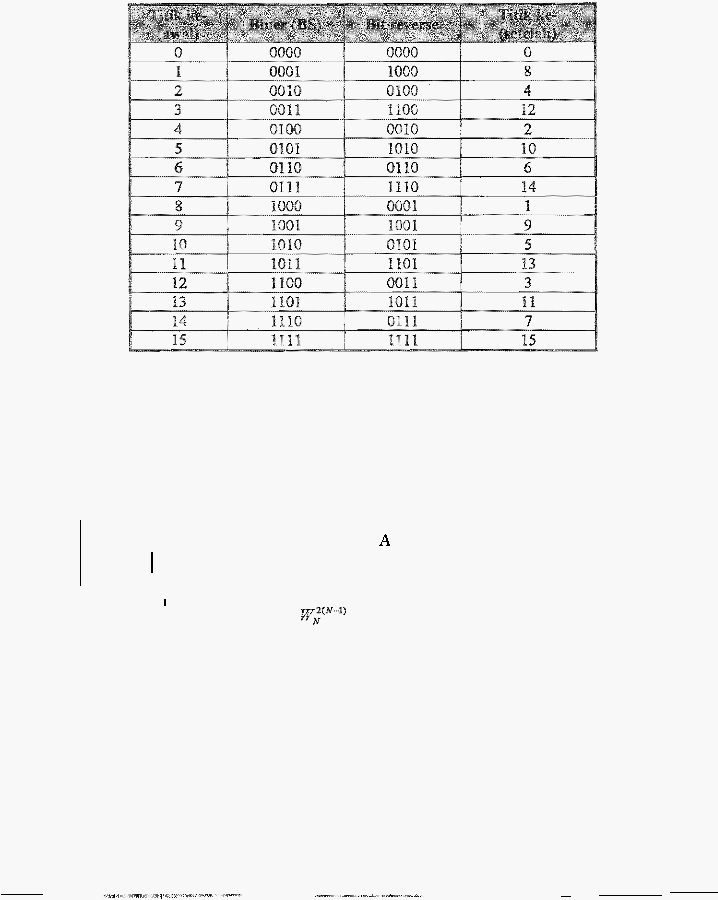
berikut.
|
 34
L
A
Tabel
2.1 Bit Revene
Pertanyaan
selanjutnya
adalah
mengapa
harus
dilakukan
bit
reverse.
Hal
ini
dapat
dijelaskan
secara
jeias
dengan
menggunakan
matriks.
Perhatikan
pers.
2.47,
persamaan
tersebut
dapat
dituliskan
dalam
bentuk
matriks sebagai
berikut :
f
X(O)
l
r
X(l)
!
I
I
I
X(2)
=c
II
W
N
"
w;
w:
W
.
N
"
.
w;
w
N
"
A
w1
N
w.:
A
w::
l
r
x(O)
l
W,{
x(l)
•
w;N
.
x(2)
I'
M
.
M
'
L
I
M
J
X(N
··l)
M
w
N
"
M
M
A
w<N-t)
vrN
WJN-t)'
[x(N-l)J
Untuk
mempermudal1, misalkan
terdapat sinyal
dengan
4-titik
yang
akan
di
D.FT,
maka
dari
2.47
diperoleh
:
X(O)
=
x(O)· w;}
+
x(l)·W::+x(2)·
W+x(3)·W::
X(l)
=
x(O)· W:+ x(l)·W+x(2)·
w,;
+x(3)·W
X(2)=x(O)·W+x(l)·
w,; + x(2)· w;
+x(3) ·
W::
X(3)
=
x(O)·
W,,;
+
x(l}·W+x(2)·
w;
+x(3)·W
|
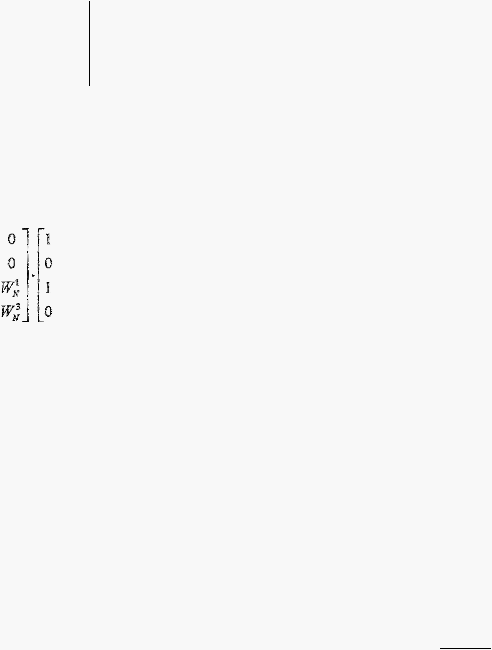 ._
J
L N
N
N
N
-
N
'"''
I
J.
'
I
35
dari hasil yang telah dijaharkan dapat ditulis daiam bentuk matriks sebagai berikut :
.
!X(O)l
jw;
w:
N
•
w;
w;1
fx(O)l
I
X(l)
1=1
W
N
'
W?
N
I
X(2)!
I
WN
w:
N
z
w:•
N
I
X(3) I
I W:"
W:'
w:•
Vi,.
!
x(l)
l
w;. I
x(2):
w;J lx(3)j
Denga11
menerapkan
sifat
periodik
yaitu
w.
n·k _
w.n·kwo<IN
dan
w;
=e-i
2
=cos(O)- jsin(O)=l
Maka
matriks di atas dapat disederhanakan menjadi
;x(o)l
fl
1
1
llfx(O)
IX(!)
=
11
ww;
w;1.!
x(I)
1
X(2)
I
1 ¹
w;
w;
w;i I Ix(2)
LX(J)j L1
w
w;
w
J
Lx(3).
Matriks segiempat di
atas
pun
masih
dapat
disederhar:takan dengan
cara difaktorkan
asalkan outputnya atan pengalinya dilakukan opernsi bit reverse. Hasil dari pewJ'aktoran
matriks di atas adalah
f
X(0)1
l
v,;;;
0
X(2)
i ¹
w,;:
o
I
X(l)
=I
0
0
1
LX(3)J
lo
o
1
o
w;
o
Hx(O)l
1
0
W:
I 1
x(l)
o
w;
o
J·
j
x(2)
j
1
o
w;
Lx(3)J
Perka!ian dua matriks yang paling kanan menghasilkan
X(O)+X(Z)·WJ\
X(l)+X(3)·W
n
4
perka!ian
dan
4
penjumlaltan kompleks.
X(O)+X(2)·Wi
X(l)+X(3)·Wi
Membutuhka
Dengan
menggtmakan sifat simetri
w:
=
-W
maka 2
perkaliannya
dapat dik:urangi,
seperti ter!ihat berikut ini:
|
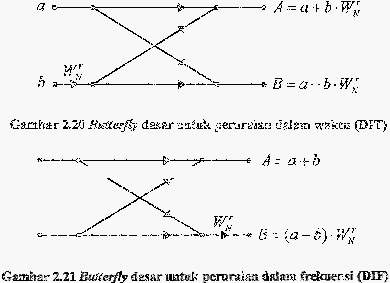 l
36
X(O)+X(2)·W \
X(l)+X(3)·W:
I
.
X(O)-X(2)·W:
Membutuhkan 2 perkalian dan 4 penjumlahan kompleks
.
X(1)-X(3)·W;
Hal serupa berlaku
untuk perkalian matriks sisanya (ingat, tadi
hanya dua matriks
yang
dikalikan) dimana dengan sifat
simetri
w
=
-w
jumlah perkalian kompleksnya dapat
dikurangi. Hasillengkap dari perkalian
tera.k.!Mr
matriks
ini
adalah
X(O)
=
(x(O)
+X(2)·W:)+W:(x(l)+x(3)W;)
X(2)
=
(x(O)+x(2)·W;)W. (x(l)+x(3)w;)
X(l)(x(O)
+
x(2) · w;)+ W
(x(l) + x(3)W;)
X(3) = (x(O)
+
x(2)·W%)- W (x(l)+x(3)W: )
Dalam
pemrosesan sinyal
digital
dikenal
isti!ah
butterfly. Butterfly
digunakan
untuk
menggambarkar, penrraian
(decimation)
yang
te!jadi. Ada
dua jenis peruraian
yang pertama
adalah pemrnian
dalam
waktu
(decimation-in-time
(DIT)) dan kedua
adalah
peruraian
da!am
frekuensi (decimation-<in-frekuensi
(DIF)).
Berikut
adalah
gambar dari butteo1y
dasar untuk kedua jenis peruraian tersebut.
|
 37
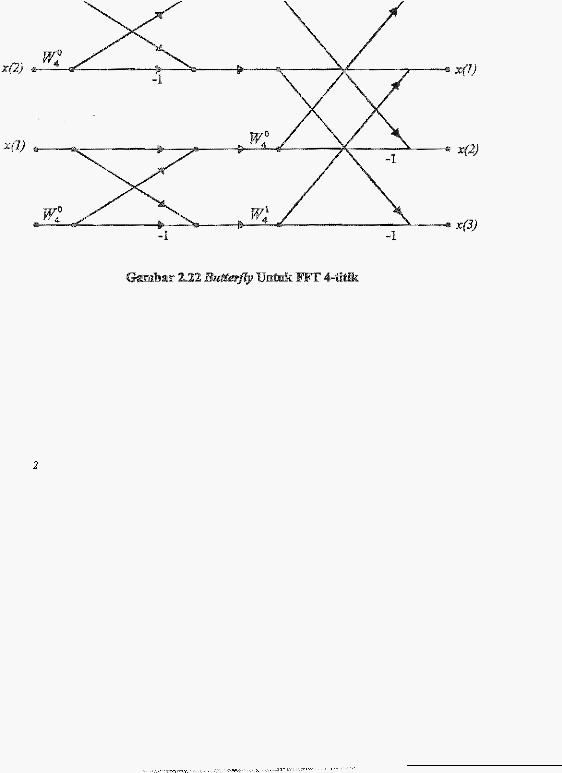
2
Hasi!
perhitungan
matriks
di
atzs
dapat
dituliskan
ulang
dengan
butterfly
seperti
terlihat
pada
Gambar
2.22.
Jenis
peru:raian
yang
gunakan
dalam
melak:ukan
perhitungan
n:atriks
tadi adalah
peruraian
dalam
waktu,
karena
yang
dilak:ukan
adalah
mengurai
inputnya
menjadi
bagian ganjil-genap.
x(O)
<>· -:----_..,11----:;f'>-· ··--...··------..-.,---e
x(O)
x(3)
Dengan
pemfaktoran,
perkalian
kompleks
yang
dibutuhkan
hanya empat
buah
bandingkan
dengan
tidak menggunakan
pemfaktoran
!:isa mencapai
16 perkalian
kompleks.
Jadi
dapat
disimpulkan
bahwa
dengan
algoritma
FFT
dimana
memanfaatkan
sifat
simetri
dan periodik
dibutuhkan
:
N*log
N
.
o
perkalian
kompleks
dan
2
o
N
*log
N
penjumlahan
kompleks
Bila dengan
perhitungan
DFT
biasa
maka
dibutuhkan
:
o
N²
perkalian
kompleks
CJ
N(N-1)
penjumlahan
kompleks.
|
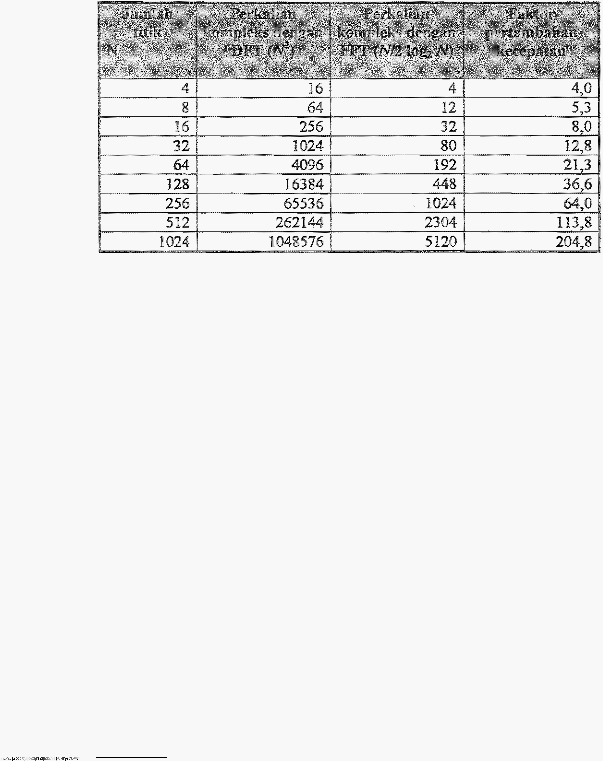 38
Berikut perbandingan
antara
perkalian
kompleks
dengan
menggunakan
komputasi
N-titik
dan
N-titik
Tabei
2.2
Ferbandingan
Antam
FFT dan
DFT
2.4
Fungsi Jertdella
(Window
Function)
DFT
menganggap
inputnya
merupakan
satu:
periode
dari
deret
yang
periodik
(Taylor,
1994,
p294). Jika
inputnya
bukan
merupakan
satu periode,
maka
akan timbul
diskontinuitas. Diskontim<itas
ini
mengakibatka\1 timbulnya
frekuell8i-frekuensi
barn
yang
menyebar
dalam
spektrum
sinyal.
Efek
disebut
dengan
leakage
atau
kebocoran.
Kebocoran
dapat
dikurangi
dengan
mengalikan
input
dari
DFT
dengan
sua.'u fungsi
yang
disebut
dengan
fungsi
window
atan
jendela.
Fungsi
jende!a menyebabkan
input
DFT
menuju
ke
di kedua
ujungnya
sehingga
diskontinuitas
tidak teJ:jadi.
Bila
spektrum
Y(m)
adalah
konvolusi
antara spektrum
sinyal
X(«#
dan
spektrum
fungsi
jendela
W(m),
maka
fungsi
jendela
yang ideal adalah fungsi
jem:lela
|
 39
)
yang
memberikan
Y(co) =X(aj}.
:Hal ini
berarti
W(aj}
=
0(
aj}
atau
w[
nl
=
I
untuk
seluruh
n
yang bukar.
merupa.l.ran fungsi
terbatas
sehingga
tidak
praktis.
Beberapa fungsi jendela
telah dikembangkan
untuk
mendekati
W(
aj}
=
0(
w)
sampai
pada
beberapa
tingk:at akurasi,
beberapa
yang
umum
adalah
:
Rectangular Window:
w(n)=l,
o
sn s
N
-1
pers.
2.48
Bartlett
Window:
i2·n
(N-1)
: -··,
OSnS-···-
f)
1
N
2
w,n
=1
)
I
2·n
(N-1
r
12---
---snslv
-1
l
N'
2
pers.
2.49
Hanning
Window:
w
(
n
)
Z· r·n'll
0.5·
[
l-eo
{
N'-l
OsnsN-l
pers. 2.50
Hamming Window:
w
·(
n
)
-
0.54
_
0.46
.
cos.
(2·7l'·
•
n\
)
'
0
s
n_ N
<
_
1
\. N-1
pers.
2.51
Blackman
Window:
wv
(
1
)
0.42-0.5-cos
(2·tr·n'l
·
1+0.08 ·cos
(4·rr·ll)
,
0
s
n
s
N
-1
pers.
2.52
N-1)
N-1
|
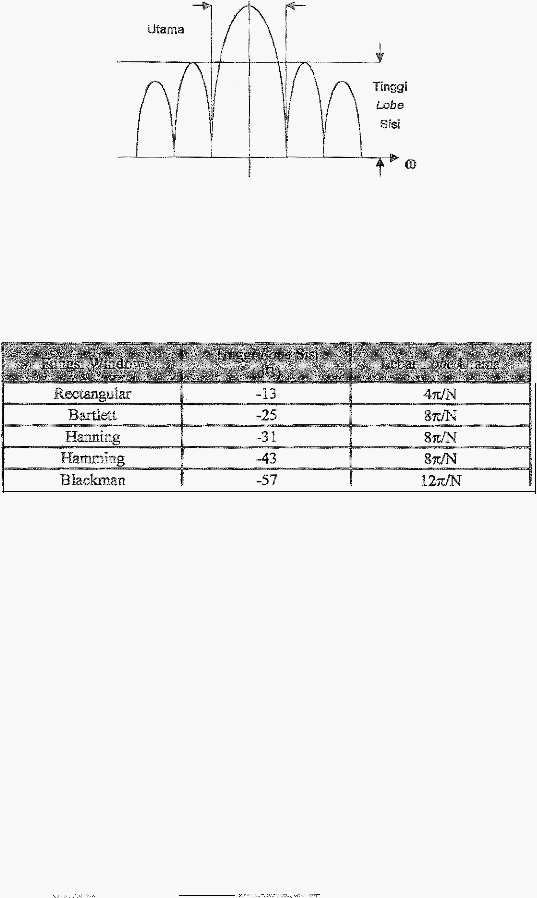 40
Lebar
Lobe
-
w(ro)
Gam bar
2.23
Kll:ralrteristik Furngsi Je.•1dela
Berikut
diperlihat.l;:an perbandingan
karakteristik
fungsi-fungsi jendela
diatas:
Ta!Jet 2.3
Kru-akteristik Fangsi-fungsi Jendeia
Untuk
mengurangi
kebocoran,
dipilih
windnw
data
w(n)
yaog
mempunyai
lobe ·sisi
lebih
rendah
dalaru
domain
frekuensi dibandingkan
dengan
windnw
persegi.
Suaiu reduksi
lobe
sisi.
dalrun fungsi
W(w)
dapat
dicapai
dengan
meiebarkan
lobe
utamanya
tetapi
mengakibatkao
spelctrum
sinyal
akao
kehilangan
resolusi.
mea spektrum
window retatif sempit lebarnya dibandingksn dengan spektrum
dari
sinyal,
fungsi
window
hanya
memberikan
pengaruh
yang
kecil
(halus)
pada
spektrum
X(w)
dan
sebaliknya.
|
 43
Dalam
pembahasan
skripsi
tersebut digunakan
fungsi
jende!a
Hanning.
Untuk
N
=
1024,
fungsi
jendela
Hanning
digambarkan:
,0.999998, I
r
•,
..
/
,C,
0
lLL.
0
200
400
600
800
moo
1024
GIJr, 2.24 Hamung Window
Filter
Digitai
Filter
pada pengolar.an
sinyal
berfhngsi
untuk
memisahkan
dan
membentuk
ulang sebuah
sinyal.
Pemisahan
sebuah
sinyal
diperlukan
bila sebuah
sinyal telah
tercampur
dengan
interferensi,
noise
dan
sinyal
lain
ya.'lg
tidak
diinginkan.
Bayangkan
kesalahan
ana!isa
yang
bisa dibuat
seorang
dokter
yang
menggunakan
alat
untuk
mengamati
aktifitas
jantung dari
seorang bayi. Ianpa
adanya filter akan
sulit
untuk
memhedakan
mana
sinyal
dari
detak
jantung
si
bayi
dengan
sinyal
yang
diakibatkan
oleh
nafas
si
ibu
dan juga
detak
jantung
ibu
tersebut.
Pembentukan ulang
sebuah
sinyal
dilakukan
bila
tetjadi
kerusakan
pada
suatu
sinya!.
Mi.salnya
pembentukan
ulang
sinyal
suara
yang
direkam
dengan
peralatan-
peralatan
berkualitas
rendah.
|
|
42
Pada umumnya
di
dalam
pengolaha11 sinyal
digital, sinyal
input dan
sinyal
output
ditampilkan
dalam
domain
waktu.
Hal
dari
pengambilan
sample
secara
periodik.
dikarenakan
sebuah
sinyal
dibenttL.lc
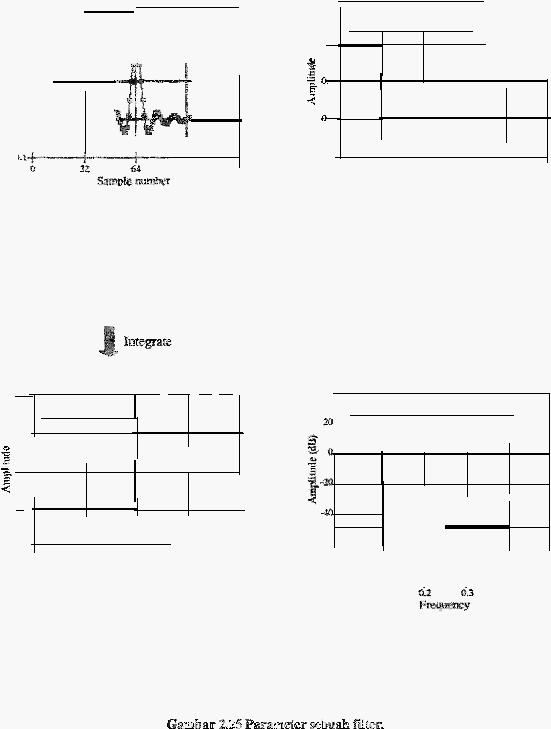
Seperti
dalam
gambar
2.25,
setiap
filter
linier
merniliki
respon
impuls,
respon
step
dan
respon
frekuensi.
Ketiga
respon
tadi
mengandung
informasi
yang
sama
mengenai sebuah filter,
tetapi
dalam
bentuk
yang
berbeda. Ttka salah
satu
ditentukan
maka
yang
lainnya
dapat
dicari. Ketiga
respon tersebut
penting
bagi
sebuah
filter,
karena
ketiga
respon
tersebut
akan
rn.enentukan bagaimana
sebuah
filter
bekerja.
Cara
yang
paling rn.udah untuk
rn.engirn.plementasikan sebuah filter adalah
dengan
melakukan
sebuah
konvolusi
terhadap
sinyal
input,
oleh
respon
impuls
dari
Filter
DigitaL
Semua
filter
linier dapat
dibentuk
dengan cam
ini.
|
 43
'
'
•
'
.
B
(l..tT:=
i
I
5
'
I
I a.
!m['lll"'l
n¢'!J<lll"'
I
1c
.
F""l'Jency r >l'()ll1<"
1
l
0.1+1--+-
-4--+-----l
!"·'r'-
•
•
-<
··"1---"i''!JJi !ft
'
l
I
!
I
•
•
5
'
'
•
•
!
6.1
(t3
05
F
n,:y
ln.
Srepr
!.0
I
A
I
I
I
120.LQg( }
!
ld·
l'r<q (inllil)
(
!
I
I
i
1
n.
i
I
I
'
•
i
l
l
'
•
N
•
....
,
•
I
I
•
Ci3
!
"31
64
Sample
1111mi:'er
"'
'
'
Cara
lain
untuk
membuat
sebuah
filter
digital
dikena! dengan
nama
"recursion."
Filter yang dibentuk dengan cara
recursion
merupakan per.gembangan dari
fHter konvolusi,
menggunakan
nilai output sebelumnya. .Filter rekursi ditentukan oleh
sekumpu!an koefisien rekursi
|
|
42
Filter yang dibentuk dengan cara rekursi biasa disebut sebagai
Infinite
Impulse
Respons
kerena respon
impuls dari
filter
ini tidak
memiliki batas. Berbeda
dengan filter
yang dibentuk dengan cara konvolusi memiliki respon impuls
yang
terbatas.
|
|
Seperti diketahui, respon
impuls adalah output dasi sebuah sistem bi!a input
dari
sistem
tersebut adalah sebual1 impuls.
Begitu
juga
respon
step adalah
output dari
sebuah
sistem bila
inputnya
adalah
step. Karena
step adalah hesaran
integrasi
dari
sebuah
impuls,
mak:a respon step
adalah
integrasi dari
respon
impuls.
Dua
cara
untu..lc
menentukan respon step dari sebuah filter adalah dengan
memberik:an
input step kepada
filter tersebut atau dengan cara
mengintegrasi respon impuls
dari
filter tersebut. Respon
frekuensi dapat ditentukan dengan menerapk.an algoritma FFT pada respon impuls.
2.5.2
Bagaimana
Informasi Ditampi!kan Da!am Sebuah Sinyal.
Informasi dalam
sebuah sinyal da!am domain waktu adalah
ketik:a
sesuatu
yang diamati terjadi dan amp!itudo dari kejadian itu
disimpan, kemudian dalam interval
waktu
tertentu diambil lagi
nilai amplitude dari kejadian
yang diamati
tersebut
Meskipun hanya l
niiai amplituda yang diambil itu tetap merupakan sebuah informasi.
Berbeda
dengan domain
waktu,
inforrnasi
yang ditampilk.an dalam domain
frekuensi
lebih sulit
untuk dibayangk:an.
Banyak hal di alam
semesta ini
teljadi secara
periodik.
Dengan jalan
mengulrur besar
frekuensi,
fasa
dan
amplituda
dari
kejadian
tersebut, maka
informasi
mengenai sistem
ya\'lg
menyebabk.an
kejadian
tersebut
dapat
dicari. Misalkan sua.-a
yang timbul ketik:a sebuah ge!as diketuk. Frekuensi dan
.amonisasi
getaran yang timbul akan berhubungan dengan masa dan keelastikan bahan
pembentuk ge!as tersebut. Kalau hanya dimi!ilri satu bua.\ nilai cuplikan saja, tidak bisa
disebut sebagai informasidari sebuah kejadian yang periodik Informasinya terdapat di
dalam hubungan dari cuplikan-cuplika;1 yang ada pada sinyal tersebut.
Hal diatas
menjelaskan betapa pentingnya respon step dan respon
frekuensi.
Respon step
menjelaskan bagaimana infurmasi
yang ditampilkan dalam domain wak:tu
|
|
|
|
45
dirubah
oleh
sistem,
sebaliknya
respon
frekuensi
menjelaskan
bagaimana informasi
dirubah
dalam domain
frekuensi.
Perbedaa.'l
ini sangatlah
penting
untuk
rnendisain
sebuah filter
karena
tidaklah mungkin
menggunakan
sebuah filter
u..t1tuk kedua tujuan
tersebut.
Kualitas
yang
baik
dalam domain
waktu
akan
membuat
kualitas
dalam
domain
.
frekuensi
menjadi buruk, bcgitu juga
sebaliknya. Kalau
ingin mendisain
filter
untuk
menghilangkan
noise
dari
sinyal
EKG
(informasinya
ditampilkan
dalam
domain
waktu),
maka
respon
step
adalah
parameter
yang
sangat penting,
dan respon
frekuensi
sedikit
pengaruhnya. Sedangkan
jika
ingin
mendisain
filter untuk
aplikasi yang
berhubungan
dengan
pendengaran, maka
respon
frekuensi
adalah
parameter
yang
sangat
penting.
Berikutnya
aka.'l
dibahas
apa
yang
membuat
sebuah filter
optimal
untuk
digunakan
dalam
domain
waktu
atau
dalam
domain
frekuensL
2.5.3
P&rameter-p:m metel!' Filter Dalam Domain Walrtu
Mungkin
kurang begitu
jelas
mengapa
respon
step penting
dalam
sebuah
filter
yang
diterapkan
dalam
domain
ftekuensi,
tetapi
respon
frekuensi
bukan
merupakan
parameter
yang
penting.
Jawabannya
terletak
pada
bagaimana
manusia
memahami
dan
mengolah
informasi
yang
ada.
Ingatl.ah bahwa
respon
step,
frekuensi
dan
impuls
mengandung infurmasi
yang
identik,
hanya saja
ditampilkan
dalam
bentuk
yang
berbeda.
Respon
step
penting
untuk
menganalisa
infurmasi
da!am
domain
waktu
karena
itu cocok
dengan
bagaimana
manusia
melihat
informasi
yang
terdapat
dalam
sinyal.
Misalkan, diberikan
sinyal
yang
sumbemya
tidak
diketahui dan
diminta
untuk
menganalisanya. Hal
yang
pertama
yang
dilakukan
dalam membagi sinyai
tersebut
keda!am
bagian-bagian
yang
karakteristiknya
sama.
Hal
tersebut
tidak
mungkin
untuk
tidak di!akukan
karena · pikiran
manusia secara otomatis
akan
mengerjakannya.
|
|
46
Beberapa
bagian
mungkin
lebih
mulus;
yang
lain
memiliki
amplituda
yang
mencapai
puncak;
yang
lain
lagi
mungkin
mengandung
noise,
Bagian
tersebut
terselesaikan
dengan
menentukan
point-point
yang
memisarJi.an
bagian
tersebut
Dari
hal
itulah
fungsi
itu
berasal.
Langkah
fungsi
tersebui
semata-mata
untuk
merepresentasikan
sebuah
divisi
antara
dua
bagi
'l
yang
sama.
Hal
tersebut
dapat
ditandai
saat
kejadian
tersebut
dimulai
atau
saat
kejadian
tersebut
berakhir,
Hal
itu
rnenjelaskan
bahwa
apa
yang
ada
disebelah
kiri
sewal'tU-waktu
berbeda
dengan
yang
ada
disebelah
kanan.
Berik:ut
ini
adalah cara
pandang
manusia
dalam
melihat
informasi
dalam
domain waktu:
sekelompok
fungsi
step
membagi
informasi
kedalam
bagian-bagian
yang
sama
karakteristiknya.
Berikutnya
respon
step
sangatlah
penting
karena
respon
tersebut
menjelaskan
perubahan
oleh
filter
yang teljadi
terhadap
bagian-bagian tersebut.
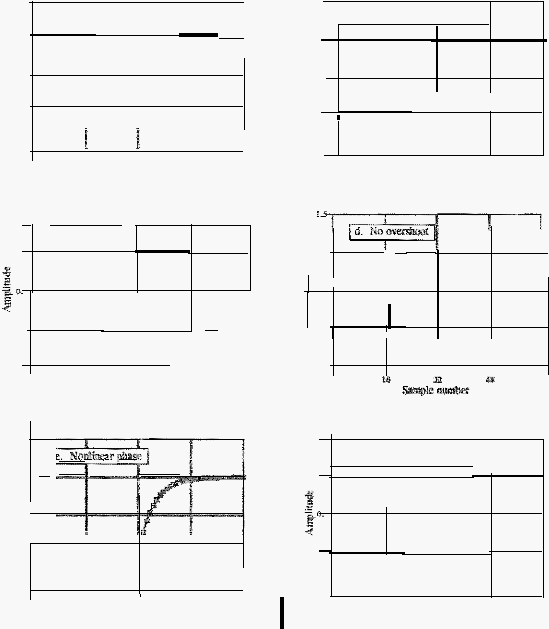
Gambar
2.26
menje!askan
pentingnya
pararneter
respon step
da!am
merancang
sebuah
filter.
Untuk
membedakan
kejadian
dalam
sinyal,
durasi
dari respon
step
h
'lls
lebih
kecil
dari
jarak
antar
kejadian.
Hal
tersebut
menyatakan
bahwa
respon
step
hams
teljadi
secepat
muP.gkin.
Hal
ini
terlihat
dalam
gambar
2.26
(a)
dan
(b).
Cara
yang
paling
umum
untuk
menentukan
risetime
ada!ah
menghiiung
jumlah
cuplikan
saat
amplitu.do
antara
I0"/o sarnpai
90%.
Risetime yang
singkat
tidaklah
selalu
mungkin
terca.?ai karena
alasan
berikut:
peredaman
noise, pencegahan
efek
aliasing
dan
lain-lain.
|
 47
r
l.
I
I
"'
""
"'
I
I
"'
u
LL
.
"
€
POOR
I
'
-!
I
GOOD
F
'S.
<l5
{ij}
"'
(l
0
J.
'
I
I
I
I
.J:J.5
AJ
5
S.."'!'!e
llll!!lbl
i
i
1
J:Z
.t
Sart¢rnn'"""
Je,
:I
!
""'
-omoer. )<
I
l
i
I
II
I
I
I
I
...!
u.
If
I
-a
'
1
.. I
!
I
i
..
I
G
?6
J1
Slmpte O'..rml>er
LS
'
I
f.
u..::.r
'*'"'
II
l
l
I
If
""
,Q,S
I
n
!'I)
S>mple Olllt'll>e<
.A
I
•5
I
I
Gambar
(c) dan (d) menunjukkan
parameter
yang
tidak
kal.ah pentingnya
yaitu
(Wershoot
dalam
respon
step.
Overshoot
haruslah dihilangkan
karena
mengubah
ampiitudo dari
cuplikan dari sebuah sinyal; hal ini adalah gangguan dasar
dari
informasi
yang terdapat
da!am
domain waktu.
|
|
48
|
|
49
Akhirnya,
tercapailab
kondisi
dimana
sisi
bawah
dan
atas
menjadi
simetris
seperti
terlihat dalam
gambar (e)
dan
(f).
Kesimetrisan
ini
dibutuhkan
agar
sudut
naik
terlihat simetris
dengan sudut
jatub.
Kesimetrisa11
ini
disebut
fusa
linier,
karena
respon
frekuensi
memiliki
fasa
seperti
garis !urus.
2.5.4
P&rameter-l;)arameter Filter Dalam Domain
Frekuensi.
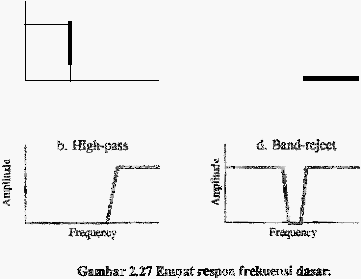
Ga..rnbar 2.27
menunjukkan
empat
dasar
dari
respon
frekuensi.
Tujuan filter
ini
untuk
melewatkan
frekuensi" tertentu,
sedangkan
disisi
lain
menindas
frekuensi
lainnya.
Band
Pass
menunjuk
kepada
frekuensi
yang
diiewatkan
sementara Band Stop
terdiri
atas
frekuensi
yang
ditindas.
Sedangkan
Band
Transisi
berada
diantara
keduanya.
Sebuah
roo!off
yang
cepat
berarti
band
transisi
sangat
tipis.
Frekuensi
antara
band
pass
dan
band
transisi
disebut
frelruensi
cut
off.
Dalam
merancang
filter
analog
frekuensi
cut
off
ditentukan
saat
penguatan
turon menjadi 0,707
(-
3dB). Filter
digital
memiliki
standar
dan
umllr"'ullya 99"/o, 90%,
70,7%
dan
50% tingkat
penguatan
mengacu
pada
frelruensi cut
off.
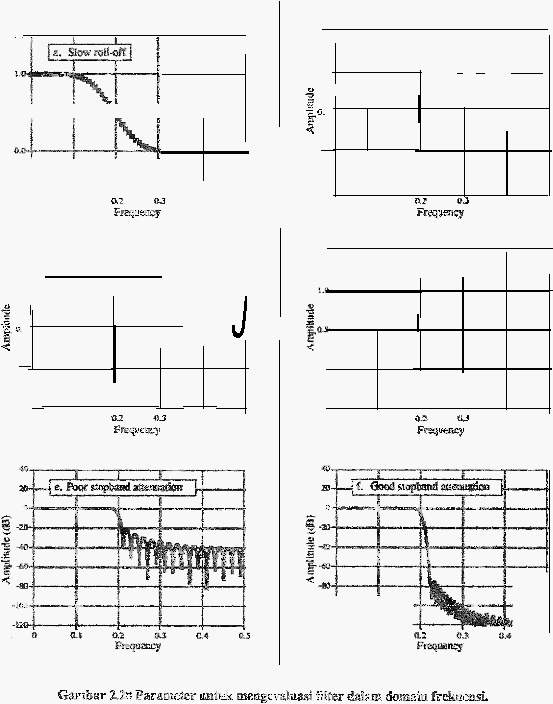
G-'o1ll.bar
2.28
memperlihatkan tiga
parameter
untuk
melihat
seberapa
baik
kualitas
filter
daiam
domain
frelruensi. Untuk
memisahkan
frekuensi
dalam
jarak
yang
sempit,
filter
tersebut
harus
memiliki
ro!l
off
yang cepat
seperti
yang
diilustrasikan
dalam
gambar
(a)
dan
(b).
Untuk
frekuensi
band
pass
dapat
bergerak
tanpa
mengalami
peredaroan,
tidaklab
diperkenankan
untuk
terjadi
ripple
Band
Pass,
seperti
teriihat
dalam
gambar
(c)
dan
(d).
Berikutnya,
untuk
meredam
band
stop
dengan
baik dbutuhkan
peredi.L.'"llall band
stop yang
baik
seperti
terlihat
dalam
gambar
(e)
dan
(f).
|
 l
<
'
49
a. Lmv·pl!!!S
c.
Baru!"!'l SS
-1!
pio%!4md:
t
.exltj.t;tf
.E
'T
l'r1il
fj
J]
"
e
'
I!
'
S!#pfJttnJ
Ft'f'G.ttt'5'..c)'
F«t,'"""'-"Y
|
|
|
 50
I
I
T
I
I
l
li
_,1
'
l
I
I
•
I
I
I
I
..
"
I
POOR
GOOD
lo
strv!l+
l
I
I
.n
'
!
"
•*--i--iiii,--4-- --
I
.._, -
.!---1---1---1---1----l
•
l
I
'
I
I
5
!
!
"
.5
i
I
I
!
1
!-
TI
l
'
I
c.
in jlOSSlla.'ld
!.5
I
la
l'J>t
I
I
I
-!
""I
I
!
j
I
i
i
I
I
I
i
I
I
I
!
I
I
'
I
I
I
I
I
I
I
•
0.1
•••
"""'
•
0.!
.,
·!00
.
.,._-J--·+
-uF.4----4----i--
05
|
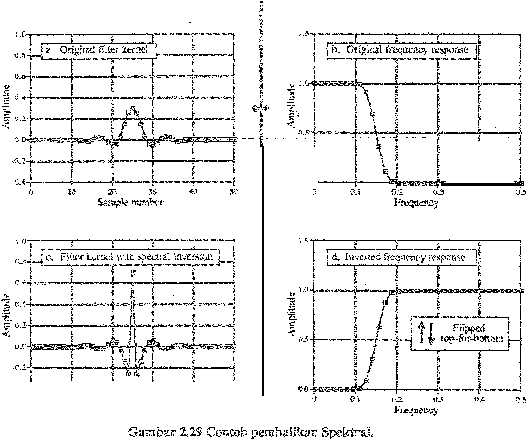 m
iu
:ro
4G
s;;J
51
Time
Domain
Frequency Domain
"' I
"·'
"·'
" +----+----r---4----4----;
{I
Somplo-
2.5.5
Filltel" High Pass, Band Pass dan Band Reject
Filter High
Pass,
Band
Pass
dan
Band
Reject
dirancang
dengan
terlebih
dahulu
merancang
sebuah
filter
Low
Pass
dan
kemudian
mengubahnya
ke
dalam
respon
yang
diinginkan.
Ada
dua
metode
untuk
mengkonversi
Filter
Low
Pass
menjadi
Filter
High Pass yaitu: spektral
invertion
dan
spektral
i-eversal keduanya
sama-sama
berguna.
Contoh
dari
spektral
invertion
terlihat
dalam gambar
2.29.
Pada
gamhar
2.29(a)
mernperlihatkan
Kernel
Filter Low Pass yang
disebut sebuah
windowed-sine.
Kernel
filter
ini
terdiri
atas
51
cupiikan,
meskipun
banyak sample
memiliki ni!ai
yang
keci! dan mendekati
nilai
no!.
Respon
frekuensi
dari Kernel
tersebut
terlihat
dalam
gambar 2.29(b),
dicapai
dengan
cara
menambahkan
l3 buah
nilai
no!kedalam
Kernel
Filter
dan
melakukan
FFT
64 titik.
Dua
hal
yang
hams
dilakukan untuk
merubah
Kernel
|
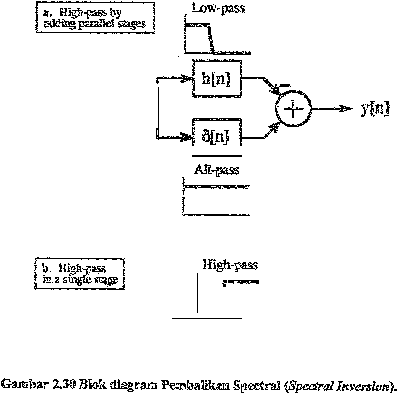 52
Filter
Low
Pass
menjadi
Kernel
Filter
High
Pass.
Pertama,
melakukan
pembalikan
tanda
pada
seriap
sample
c!ari
Kernel
Filter.
Kedua,
tambahkan
satu
kedalam
cuplikan
yang
berada dipusat simetri.
Kernel Filter High Pass yang dihasilkan terlihat
pada
gambar
2.29(c)
sedangkan
respon
frekuensinya
pada
229(d).
Spektrallm>ertion
menukar
respon
frekuensi
atas
menjadi
bawah
dan
sebaiiknya,
Membah
Band
Pass
menjadi
Band
Stop
dan
Band
Stop me!'Jadi
Band
Pass.
Dengan
kata
Jain
spektal
invertion
merubah
filter
dari
Low
Pass
menjadi
High
Pass,
High
Pa.<:S menjadi
Low
Pass,
Band
Pass
menjadi
Band
Reject,
Band
Reject
menjadi
Band Pass.
x[n]--1
x[n]
--ll>lil!>l
O(n] - b[nJ
!---'
>' >
y[n]
Gambar
2.30
memperlihatkan
kedua
penggubahan
tersebut
terhadap
domain
waktu
didalam
spektn1m
frekuensi
yang
dibalik.
Dalam
gambar
2.30(a)
sinyal
input,
x[n], dan
memungk:inkan
untuk
dua
sistem
secara pararel.
Satu
sistem
merupakan
Low
|
|
53
Pass
Filter,
dengan
memberikan
respon
impuls
oleh
h[n].
Sistem
lainnya
tidak
memberikan .respon kepada
sinyal,
dan. karena
itu
fungsi
delta
mernpakan
respon
impuls,
S[
n}.
Output keseluruhan,
y[
n
J,
adalah
sama
dengan
output
minus
dari
seluruh system
pass.
Saat
komponen
frekuensi
rendah
mengurangi
sinyal
aslinya,
hanya
komponen
frekuensi
tinggi
yang
tampak
pada output.
Demikianlah
filter
high
pass
terbentuk.
Hat
tersebut
dapat
pula
dibentuk
seperti
operasi
dua
tingkat
dalam
program
komputer:
Ja!ankan
sinyal
me!a!ui
filter
low
pass,
dan
kemudian
kurangi
sinyal
filter
dari
sinyal
aslinya.
Tetapi,
seluruh
operasi
dapat
dibentuk
pada
tingkatan
sinyal
dengan
menggabungkan dua
kernel
filter.
Sistem
parallel
dengan
penambahan
output
dapat
menggabungkannya
pada
tingkatan
sinyal
dengan
menjumtahkan
respon
impulsnya.
Seperti
yang
tergambar
pada
2.30(b),
kernel
filter
untuk
filter
high
pass
diberi
an
o!eh:
li[n]-
h(n].
Hal
tersebut,
merubah
tanda
untuk
semua
sample,
dan
menambahkan
satu
pada
sample
pusat
simetri.
Untuk
teknik
ini
bekerja,
komponen
frekuensi
rendah
yang
merupakan
bentukan
dari
filter
low
pass
hams
memiliki
fase
yang
sama
seperti
komponen
frekuensi
rendah
yang
terbentuk oleh
semua
sistem
pass.
Sebaliknya
pencapaian
pengurangan
tidak
mengambil
tempat.
Berikut
merupakan
dua
batasan-bataaan
pada
metode:
(1)
Kernel
filter
aslinya
harus
memili.ki simetri
kiri-kanan,
dan
(2)
impuls
harus
ditambahkan
pada
simetri
pusat.
Metode
kedua
untuk
konversi
dari high pass
ke
low
pass,
spectral
reversal,
dili!ustmsikan
pada gambar
2.31.
Seperti sebelumnya,
kernel
low
pass pada gambar
2.3l(a)
yang
berhubungan
dengan frekuensi
respon
pada
gambar
2.3l(b).
Kernel
high
pass,
g!!l!lbar
2.31(c),
terbentuk
dengan
menggubah
tanda
pada
setiap
sample
dalam
gamhar
2.31(a).
Seperti
pada
gambar
2.31(d),
membalikkan
domain
frekuensi kiri
untuk
|
|
|
|
|
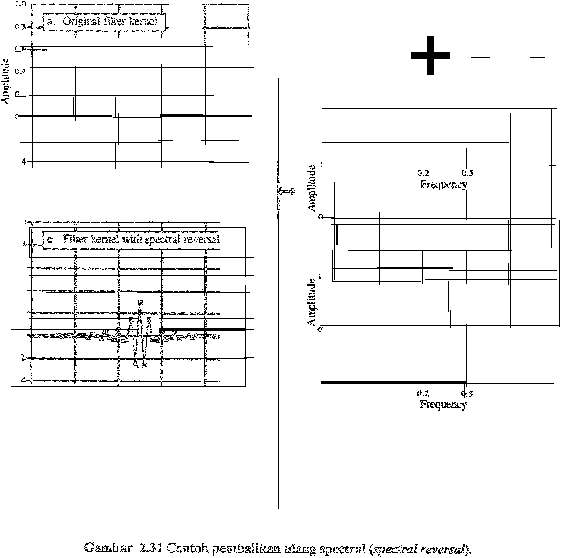 54
·+··*·
I
"'
"'
""
""
ti
u
I
.
4
"
.
kanan:
0
menjadi
0,5
dan
0,5
menjadi
0.
Frekuensi cutoff
pada
contoh filter
low
pass
adalah
0,15, hasil pada
frekue11Si
cutoff
dari filter
high
pass
menjadi
0,35.
Time
Domain
•
I
I
---r
'
i;t.,
l
\
Frequency Domain
oal
frequwcy ._"""
I
\
l
'
I
'
t
i
I
l
•
.•
\'
J
J
I
a
10
'
Sample llll.'llter
6.1
•••
L
.
0
.
u
:Ze
.0:
i
{).2
0
-<!
.5
1
R"'"""-"<1
freqm..cy
••
l
I
I
11
1/
_,
/<fr{j4ight
t
-<'!
•
10
"'
!llll
"
l'-
'
..
"'
O.l
o.•
S.rup!"
Mengubah
tanda
untuk
setiap
samp!enya
memiliki
kesamaan
dan
untuk
menggandakan
kernel
filter
dengan
frekuensi
pada
0,5.
Akhirnya,
gambar
14.8
dan
14.9
menjeiaskan
bagaimana
kernel
low
pass dan high
pass
dapat
digabungkan
kebentuk
b;uu:l
pass
dan
filter
band
reject.
Menjumia.bkan
kernel
:filter
menghasilkan
filter
band
pass.
|
 !
Moving
aver-oge (Ch. 15)
Single pol
(Cil.
>9)
Wzm:!owed-sinc (Ch. 16)
Ciltlbyshev
(C!I. 20}
I
HR
custom (Ch. 17)
Iterative dc.<dgn
(Cil. 26)
55
2.5.6
Kiasifikasi
Filter.
FILTER IMPLEMENTED BY:
---,
I
TimeDomll;in
(,smoolhfR8. DC Yt!Jf'IOW1f)
Freqooncy
Domaill
(>'Pf'mtl•gfnH{rutlcks)
Cust0!1l
(l!eCOIIWJiMi<'II'
('-')moludon
Fmii< ll!IP•L<<
llespo
.-
(l(l/1)
Rllcursi\lll
bifirrire
•lui
(fJRJ
Pada
gambar
2.32 ditampillam
bagaimana
:filter digital
dik!asifik:asikan
oleh
kegunaannya
dan
oleh
implementasinya.
Penggti<'Jaall
digital
filter
terbagi
atas
tiga
k:ategori:
time
domain,
frequency domain
dan
custom.
Seperti yang
digambarkan
pada
sebelumnya,
filter
time
domain
digt.makan
saat
informasi
di-encode
daiam
bentuk
sinyai.
Filterisasi
time domain
digunakan
untuk:
smoothing,
DC
removal, dan
lain-lain.
Pada
perbedaanya,
filter
domain
frekuensi
digunakan
bila
informasi
berisi
amplituda,
frelruensi
dan fase
dari
kornponen sinusioda.
Tujuan
dari
filter
ini
adalah untuk
memiaahkan
aalah
sara
dari
band
frekuensi dengan
yang
lainnya.
Filter custom
digunakan untuk
peketjaan khusus
yang dibuturJi:ar1
oieh filter,
sesuatu
yang
lebih
rumit
daripada
cmpat
respon
dasar
(high
pass, low
pass,
band pass dan
band
reject).
Digital
filter
dapat
di.implementasilam
dengan
dua
cara.
Dengan
konvolusi
(FIR
atau
Finite
Impulse
Response)
dan
dengan
rekursi
(UR
atau
Infinite
Impulse
Response).
Konvolusi
membawa
filter
dengan perfurma
yang
lebih
baik
dibanding
dengan
menggunakan
rclcursi, tapi
tmtuk
mengeksekusinya
jauh
lebih !ambat.
|
 56
pengertian
dasar
tentang
filter
yang telah
dibahas,
maka
dapat
ditarik
kesimpu!an
untuk
membuat sebuah
equalizer
dibutuhkan
sebuah
filter
digital
yang
bekerja
pada
domain
frekuensi.
Hal
berarti
filter tersebut adalah
filter windowed-sine
(FIR)
atau Chebyshev
(I!R).
Dari
dua
filter
diatas
maka
1.mtuk
sknpsi
ini
digunakanlah
filter
wiruiawed-sinc
karena
kemampuannya
yang
lebih
bagus
dacripada
filter
chebyshev. Karena
hal
ini
juga,
maka
pembahasan
berikutnya
tentang
filter
hanya
mengenai
filter
windowed-sine.
Sedangkan
untuk
jenis filter
yang
lain
tidak
dibahas
pada skripsi
ini.
Filter
Windows Sine
Filter
windowed-sine
umum digunakan
untuk
memisahkan
band frekuensi
satu
dengan
yang
lannya.
Filter
ini
sangat
stabii
dan
rnemiliki
performa yang
sangat
bagus.
Filter
ini
menngunakan
metode
konvolusi
standart
sehlngga
cukup
mudah
untuk
memprogramnya tetapi
lambat
dalam dijalank:a..'L
Drum.r Filter Windowed-Sine
Gambar
2.33
menjelaskan
maksud
dari
filter
windows
sine.
Pada
gambar
(a)
diperlihatkan respon
frekuensi
dari
filter
low
pass
yang
ideaL
Semua
frek:uensi
dibawah
frekuensi cutt-off
(
fc)
dilewatkan
dengan
gabungan
amplituda, sedangkan
semua
frekeunsi
tinggi diblok
Frekuensi
yang
dilewatkan
benar
benar
datar,
pelemahan
dalam
frekuensi
yang
ditaharr
tak
terhlngga
nilainya. Dan
transisi
antara
keduanya
sangat
kecii.
Menggunakan metode
Inverse
Fourier
Transform
dari
respon
frekuensi
ideal
ini
menghasilkan
filter
kernel yang
ideal ( respon
impulse), ditunjukan
pada gambar
(b).
|
 57
Kurva
dalam
bentuk
un1um
:
sin
(x)/x
,
dinamakan
fhngsi
sine
ditunjukan
oleh
persamaan
dibawah
irri :
h[iJ -
pers.
2.53
Melakukan
konvolusi
terhadap
sinyal
input
dengan
kernel
filter
ini akan
menghasilkan
filter
low-pass
yang
sempume.
Yang
menjadi
masalal1
adalah: fhngsi
sine
ini
ber!anjut
terus
berosilasi
dalarr: sisi
positif
dan
negatif
sampai
tak
terhingga,
sehingga
tidak pernah
mencapai a.'llplitudo
no!.
Panjang
yang
tak terhingga
ini
bukan
masalah
bagi
perhitungan
matematika,
tetapi
bagi
komputer
ini
merupakan masalah.
Untuk
mengatasi
masalah ini
harus
dibuat
dua
perubahan
fungsi
sine
dalam
gambar
(b),
hasH
bentuk
gelombang
ditunjukkan
dalatn
gambar
(c).
Pertama,
dilakukan
pemotongan
sampai
dengan
titik
M-1
,
secara
simetri
sampai
ujung
yang
utama
dimana
M
adalah
bilangan
genap.
Semua
sample
diiuar
dari
titik
M-l
diatur
menjadi
bernilai
0
atau
sama
dengan
diacuhkan.
Kedua,
seluruh
nilai
digeser
ke
sebelah
kanan
sehingga
dimulai
dari
0
sampai
M.
Hal
ini
membuat
kernel
filter
dapat
di.representasikan
dengan
indeks
positif
Sementara b&'"!yak bahasa
progr&'!'.rning
mengijinkan
indeks
negatif sehingga
ba!uisa
programming
tersebut
susah
untuk
digunakan.
Efek !anjutan dari pergeseran
sebesar M/2 pada filter kernel
adalah
mengeser
sinyal
keluaran
deng&'l besar
yang sama.
KareM
perubahan
kernel
filter
yang
terjadi
hanyalah
perkiraan
dari
kernel
filter
yang
ideal,
maka
tidak
tercapai respon
frekuensi
yang
ideal. Untuk
mendapatkan
respon
frekuensi,
maka
dilalrukan
transformasi
fnurier
terhadap
sinyal
dalam
gambar
(c),
menghasilkan
lrurva
dalam
gambar
(d).
Yang terjadi
kemudian
adalall sesuatu
yang tidak
|
|
58
diinginkan.
Terdapat
riak
yang sangat
banyak
dahun
frekuensi
yang
dilewatkan
dan
pelemahan
yang
lemah
dalam
frekuensi
yang
ditahan.
!YJJtsa!ah
ini
berasal
dari
ketidak
kontinuan
yang
terjadi
secara
tiba
tiba
di
akhir
dari
fungsi
sine
yang
dipotong.
Dengan.
menambah
panjang kernel
filter tidak
akan
menyelesaikan
masalah
ini,
karena
berapapun
panjangnya M yang
dibuat
sangat
tidak
berpengaruh.
Untungnya,
ada
metode
sederhana
untuk
mengatasi
masalah
ini.
Gambar
(e)
menunjukkan
kurva
yang
ha!us
yang
dinamakan
Blackman
wind.aw.
Memperbanyak
pemotongan
sine
ditunjukkan
pada
gambar (c),
dengan Blackman
wind.aw,
hasil
dari
filter
window
sine
dimuncul.kan
pada bambar (f).
tujuannya nntuk
menghindari
pemotongan
yang
curam
dan
tiba
tiba
dan
dengan
demik:ian
meningkatkan
dapat
respon
freku.e:JSi.
Gambar
(g)
menunjukkan
peningkatan
ini.
Frekuensi
yang
lewat
sekarang
adalah
datar,
dan
attenuasi
frekuensi
yang
ditahan
sangat
bagus
tetapi
tidak
dapat
dapat
dilih..at
pada
grafik.
Ada
beberapa
window
yang
berbeda
yang
lain,
banyak
dari
window
tersebut
dinama..l(:an
dari nama akhir
penemunya
pada
tahun 1950 an.
Hanya
Hamming
windaw
yang
digunakan
dalam
skripsi
ini.
Dibawah ini
terdapat persarnaan
kedua
window
tersebut:
w[i]
=
0.54- 0.46cos(2nt/M)
pen;.
2.54
Gatnbar 2.34
menunjukkan
bentuk
dari
hamming
window
dan
blackman
wir.dow
untuk
M=SO.
V\l!ndow
mana
dari
kedua
window diatas yang
lebih
baik
?
Hal
tersebut
terg-antung
parameter.
Seperti
pada
gambar
2.34(b)
Hamming
windaw memiliki
roll-off
20% lebih cepat
dibandingkan
Blackman
window.
|
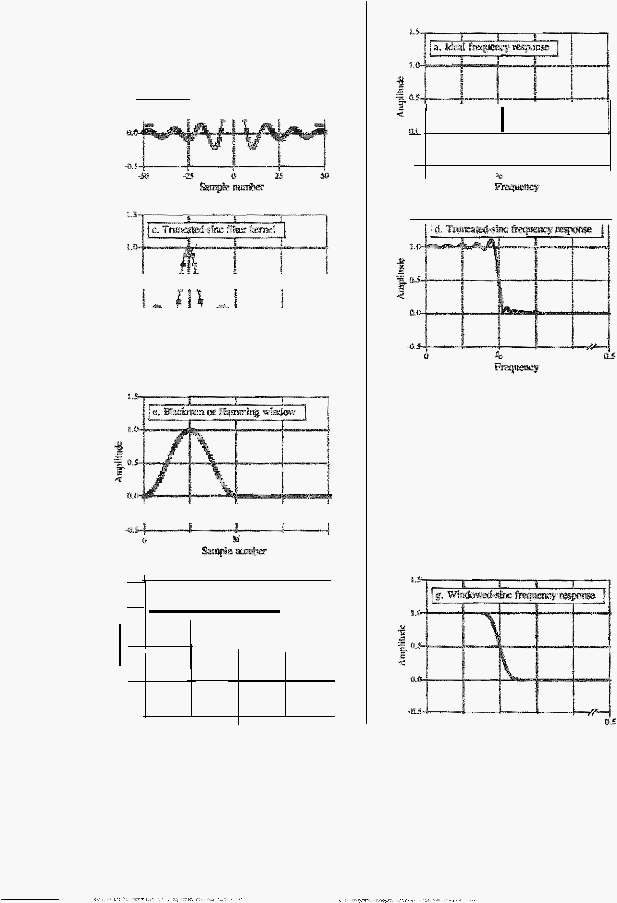 "'
'
L
!.
59
Time Domain.
u
jib. l:ii>Jl
rer J
I
1'-'
i
!
I
Frequency Domain
U.5
-,-ffi-• ---·
<1
I
i
'
•
I
I
I
I
'
!
•
•
!
I
I
•
I
l
'
I
•
.
l
"
·
tu . - M---+----+----
"'
"-•!!!!: -""
emm"
If.
Wi ··lllo.-:7""-
I
-
!
!J.f
...
j-1
I
v
v
I
M
""" """''Y
GOiillbar 1.33 PII"O!leS pembentukan kernelfilter
windowed-sine
|
 I
l
I
I
I
-
!
I
I
I
IM
•
•
,_,I
60
'
1•
,
'-"
,
'"" "I
,
I
j
1
,llla-, !
I '-'"
I
i
-t--
'
l
I
I
I
\
'
'
I
I
I
Q.
'
it.;t
G,)
f""'l'let!CY
Gambar 2.34 Kalrakteristik
!uummint;dan
bloc/arum
window
Bagaimanapun
gambar c
menunjukkan
bahwa
Blackman
window memi!iki
hasil
frekuensi
yang
ditahan
yang
!ebih
baik.
Untuk
lebih
pastinya
frekuensi
yang
ditaban oleh
Blackman
window
berkisar
-74
dB
(
-
0,02%
),
Sementara
Hamming
Window
lumya
berkisar -53dB ( - 0,2
%
).
Walaupun
tidak
dapat di!ihat
pada
grafik
diatas
Blackman
window memiliki
riak
riak
pada
frekeunsi
yang
dilewatkan
hanya
0,02
%,
Sedangkan
Hamming
window
hanya
0,2
%.
Secara
garis
besarnya
Blackman
window
seha.'Usnya menjadi pi!ihan pertama sebab
pergeseran
yang
lambat
lebih
mudah
ditangani
dari
pada
yang
memi!iki frekunsi
taba.n yang
!ebih
buruk.
Ada
beberapa
window
yang
mungkin
ingin
diketabui,
walaupun
sangat
jauh
hila
dibandingkan
dengan
Blacknu.m
winder"'
dan Hamming
window. Seperti
Bartlett
window yang
berbentuk
segitiga,
menggunakan
garis lu.rus secara langsung. Hanning
|
 61
window
disebut
juga
raised cosine
window
didapat
dari
Kedua
windows
ini
mempunyai
kecepatan
roll off seperti
Hamming,
tetapi lebih
jelek atenuasi
frekwensi
yang
dital1annya.
(Bartlett:-25dB
atau
5,6%,
Hanning-44dB
atau
0,63%).
Selain
itu
juga
ada
rectangular
window.
Ini
sama
seperti
tidak
ada
window,
hat1ya
te!jadi
pemotongan
pada
ujung
akhimya
seperti
pada
gambar
!6/lc.
Sedangkan
pergeserannya
-2,5
kali
lebih
cepat
dati
Blackman,
atenuasi
frekwensi
yang
ditahannya
hanya
sekitar
-2ldB
(8,9%).
2.5.7.2
Peraneangan
Filter
UntUk merancang
filter
windowed-sine,
2
paramater
yang
harus
dipilih
adalah
frek:wensi
cutofl'Jc,
dan
paujang
dari
kernel
filter
(M).
Frekwensi
cutoff
bersifat
seperti
pecahan
dati sampling
rate
maka
nilainya
harus
antara
0
dan
0,5.
:Nilai
untuk
M
sehan:ling
atau sesnai
dengan
apmksimasi berikut
ini ;
per;.2.55
Dimana
BW
adalah
Iebar
dari
frekwensi
transisi, ukuran
dati
dimana
kurva
tertinggai
satu
yang
kosong,
hampir
mendekati
0
(kurva
dati
99"/o-1%). Lebar
frekwensi
transisi
juga
bersifat
seperti
pecahan
dari
frekwensi
samplit-;g dan harus
bernilai
antara 0
dan
0,5.
Gambar
2.35(a)
menunjukan
contoh
bagaL'llana.
aproksimasi
ini
digunakan.
Tiga
kurva
yang ditunjukan
didapat
dari
kernel
filter
dengan M=20,40,dan
200. Dari
persamaan
16/3
Iebar frekwem;i
transisi
adalh
BW=0,2
,
0,I
,
dan
0,02
,
masing-masing.
Gambar
(b)
menunjukkan potongan drui
respon
frekwensi
tidak
tergantung
pada
frekwensi
cutoff
yang
dipilih.
|
 I
'
I
62
3
(1>.
R¢11-•o.(' taff oi:y
11
'
i
I
I
l
5l
"
I\ """""'
!
"
..,.I
I
'
'
I
'
I
I
:
I
.
I
i
I
-
lr #l
OJ:t+---+--
l
\I
I
\I
'
'
I
\
U
{U
13.1
f.tl
'
'
Freq \IDey'
Sejak
dibutu.lhlcan untuk
konvolusi
yang
proposiona!
pada
panjang
sinyal,
persamaan 2.55
menunjukkan
hubungan
antara
waktu
perhitungan
(tergantu.ng
pada nilai
"M) dan
ketajaman
filter
(nilai
BW).
Sebagai
contoh,
20"/o
pergeseran
yang
lambat
dari
Blackman window (seperti
yang
dibandingkan dengan
Hamming)
dapat digantikan
dengan
menggunakan kernel
filter
20%
lebih
banya.lc dengan
kata
lain
dapat
dikatakan
Blackman window 20%
lebih
lambat
untuk
mengerjakan ekuivalen
roll-off
Hamming
>vindow.
lni
penting karena
kecepatan pengerjaan dari
filter
window-sine
sudah
termasuk lambat.
Seper'J
terlihat
pada Gambar 2.3S(b),
frekuensi
cut-off dari.
filter >vindow-
sine diukur
pada satu
seteP,gah titik amplituda.
Mengapa
menggunakan
0.5
pengganti
dari
sta\'ldar
0.707
(-3db)
digunakan
dalam elektronika
analog
dan
digital
filter
yang
lainnya?
Ini
karena.
Respon
frekuensi
>vindow-sinc
berbentuk
simetris
antara
frekuensi
yang
dilewatkan dan
frekuensi
yang
ditahan
seoagai
eontoh,
basil
Hamming
window
pada
riak
frekuensi
yang
dilewatkan
dari
0.2%
dan
atenuasi
frekuensi yang
ditahan
dari
0.2%.
Filter
yang
lain
tidak
menunjukk:an simetri
seperti
ini
dan
selain
itu
tidak
terdapat
keuntungan
memakai
satu
setengah titik
amplitudo
untuk
membuat
frekuensi
menjadi
|
|
63
cut-off
sepcrti
yang
telah ditampilkan
pada
chapter ini,
simetri
ini
membuat
window-
sine
coook
untuk
spectral inversion.
Setetah
fc
dan
M
telah
dipilih,
kernel
filter
akan
menghltung
dari
persamaan
dibawh ini :
-
0
.....
C
(
O
2r;;f)
't
!lOScos
pers.
2.56
47!;)
l
\
M
(
1
Berdasarkan
pembahasan
sehamsnya
telah
dikenali
tiga
komponen : fungsi
sine, ¥,12
shift,
dan
Blackman
Window.
Pada
filter
untuk
mendapat
suatu
pengnatan
pada
DC,
nilai
K
yg
tetap
hams dipilih
seperti
penjum!ahan
dari
semua
sampel
adalah
sama
dengan
satu. Untuk
latihan,
abaikan
K
pada
saat
perhltungan
kernel
filter
kemudian
dinormalisasikan
semua
sampel
yang dibutuhkan.
Juga
abaikan
bagaimana
perhitungan
tersebut
ditangani
ditengah-tengah
sine,
I =
M/2,
dimana
yang
terlibat
dibagi
dengan
no!.
Persamaan
ini
mungkin panJang,
tetapi mudah
untuk digunakan
dapat
dengan
mudah
ditulis
kedaiam
program
komputer, dan
biarkan
komputer
menangani
perhitungan
tersebut.
Jika
pcrsamaan
ini
dicoba
untuk
dianalisa
dengm
tangan
maka
yang
di!akukan ada!
a,\ hal
yang
benar-benar
sa!ah.
Persamaan
2.56
mePJelaskan
!ebih
l
'ljut
tentang
kernel
filter
yang
ber!okasi
didalam
komputer
array.
Sebagai
contoh,
M
dapat
dipilih
sampai
seratus.
Untuk
diingat,
M
harus
dalam
bentuk
bilangan
genap.
Poin
pertama
daiam
kernel
filter
adalah
didalam
!okasi
array
nol,
sedangkan
poin
terakhir pada
lokasi array
seratus.
Ini
berarti
ba.'J.wa
par
ang
input
signal
adaiah
seratus satu
titik.
Pusat
dari
simetri adalah pada
poin
lima
puluh,
M/2.
Lima puluh
titik yang
berada dikiri
simetri dengan
lima
puluh titik
yang
|
|
64
berada dikanan.
Titik
no! mempunyai
nilai
yang
sama
dengan
titik
seratus,
dan
titik
empat
sembilan
mempunyai
nilai
yang
sama
dengan titik
lima
puluh satu.
Jika
mempunyai
nomor
yang
spesifik
dari
filter
kernel, seperti
menggunakan
FFT,
dapat
dengan
mudah
menambahkan
no!
pada
satu dan
yang
lainnya.
Sebagai
contoh,
dengan
M
=
100, dapat
membuat
sampel 101
me!alui
127
sama dengan 0,
hasil
dalam
filter
kernel
128
poin
panjangnya.
|