 BAB 5
HASIL DAN PEMBAHASAN
5.1
Penyajian Data
Tabel 5.1 Total Hasil Penjualan
Bulan
Total Hasil Penjualan
(dalam jutaan rupiah)
Jan-04
59.
Feb-04
49.
Mar-04
57.
Apr-04
53.
May-04
56.
Jun-04
60.
Jul-04
65.
Aug-04
53.
Sep-04
56.
Oct-04
66.
Nov-04
5
Dec-04
5
Jan-05
67.
Feb-05
58.
Mar-05
66.
Apr-05
61.
May-05
58.
Jun-05
64.
Jul-05
51.
Aug-05
60.
Sep-05
50.
Oct-05
66.
Nov-05
51.
Dec-05
66.
Jan-06
48.
Feb-06
65.
Mar-06
55.
Apr-06
53.
May-06
50.
Jun-06
65.
Jul-06
52.
Aug-06
62.
Sep-06
52.
Oct-06
54.
Nov-06
61.
|
|
43
Tabel 5.1 diatas menunjukkan data total hasil penjualan yang diperoleh oleh Optik
Ambasador mulai Januari 2004 hingga November 2006, dengan bulan sebagai variabel
bebasnya dan total hasil penjualan sebagai variabel tak bebasnya.
5.2
Pengolahan Analisis Data
5.2.1
Brown’s Double Exponential Smoothing
5.2.1.1
Inisialisasi Variabel
Inisialisasi nilai awal untuk perhitungan menggunakan metode ini
'
"
dilakukan untuk memberi nilai awal pada variabel
S
1
,
S
1
,
a
1
,
b
1
dengan
menggunakan
persamaan
3.2.1.6,
3.2.1.7,
dan
3.2.1.8,
dengan
menggunakan data dari tabel 5.1, akan diperoleh nilai sebagai berikut:
'
"
S
1
= 59.2,
S
1
= 59.2, a1
=
59.2, b1= -7.25.
5.2.1.2 Menentukan Nilai Optimal Parameter
a
Dari
hasil
inisialisasi
parameter
di
bagian
sebelumnya,
dengan
menggunakan
iterasi
untuk
data
dari
tabel
5.1
menggunakan
persamaan
3.2.1.1, 3.2.1.2, 3.2.1.3, 3.2.1.4, dan 3.2.1.5, akan diperoleh nilai parameter
a
yang
optimal
sebesar
0.02.
Hasil tersebut
diperoleh
dengan
membandingkan nilai MAPE dan MSD dari tiap-tiap iterasi
menggunakan
nilai
a
yang berbeda-beda
antara 0
hingga
+1.
MAPE
dan
MSD
dapat
diperoleh menggunakan persamaan 3.3.3 dan 3.3.5. Untuk nilai
a
=
0.02,
MAPE
yang didapatkan adalah 9.003, dan MSD
yang didapatkan adalah
34.687. Perhitungan lengkapnya disertakan di lampiran.
|
|
44
5.2.1.3
Model
Peramalan
dari
Brown’s
Double
Exponential
Smoothing
Dengan hasil yang diperoleh dari bagian sebelumnya, akan
didapatkan pemodelan deret waktu pada nilai t = 35, menggunakan
persamaan 3.2.1.5 untuk metode ini adalah sebagai berikut:
F
35+
m
=
58.146 + (-0.00921)m
(5.2.1.3.1)
Dimana m
merupakan
rentang
waktu peramalan
(forecast horizon)
yang
digunakan untuk meramalkan periode ke-t+m.
5.2.2
Holt’s Two-Parameter Trend Model
5.2.2.1
Inisialisasi Variabel
Inisialisasi nilai variabel untuk metode ini dengan menggunakan
persamaan
3.2.2.4
dan
3.2.1.8
untuk
data
dari tabel 5.1, diperoleh nilai
sebagai berikut:
S1
=
59.2, dan b
1
=
-7.25.
5.2.2.2
Menentukan Nilai Optimal Parameter
a
dan
ß
Menggunakan
nilai awal S
1
dan b1
tersebut, akan diperoleh
nilai-
nilai S
t
dan b
t
selanjutnya, dengan melakukan iterasi nilai variabel
a
dan
ß
menggunakan persamaan 3.2.2.1, 3.2.2.2, dan 3.2.2.3, akan diperoleh nilai
a
yang optimal
sebesar 0.3, dan nilai
ß
yang optimal sebesar 0.43. Nilai
tersebut menghasilkan nilai MAPE sebesar 12.983, dan nilai MSD sebesar
78.855. Perhitungan lengkapnya disertakan
di lampiran.
|
 45
5.2.2.3
Model Peramalan dari Holt’s Two-Parameter Trend Model
Dengan hasil perhitungan yang didapatkan dari bagian
sebelumnya , dengan menggunakan persamaan 3.2.2.3, pemodelan
data
deret waktu yang didapatkan untuk periode ke-t+m, dengan t = 35 adalah
sebagai berikut:
F
35+
m
=
57.3796 + 0.355(m)
(5.2.2.3.1)
Dimana m merupakan rentang waktu peramalan (forecast horizon).
5.2.3
ARIMA (AutoRegressive Integrated Moving Average)
5.2.3.1
Perhitungan Autokorelasi (ACF)
Dengan menggunakan persamaan 3.2.4.1.1 untuk data pada tabel
5.1, akan diperoleh nilai ACF dari lag 1 hingga 9. Tabel 5.2 menunjukkan
hasil perhitungan ACF.
Tabel 5.2 Nilai ACF
Lag
ACF1
-0.46501
0.330384
-0.15619
0.179174
-0.25098
0.266531
-0.23345
0.182547
-0.01545
Dengan membandingkan
nilai
ACF terhadap selang kepercayaan
95% (
a
=
5%), yang diperoleh dengan menggunakan persamaan 3.2.4.1.2,
|
 46
dengan
nilai Z adalah 1.96 dan n = 35, akan didapat
selang kepercayaan
berikut:
-
0.3313 = ACF (k ) = 0.3313
Jika
nilai ACF dimasukkan
ke
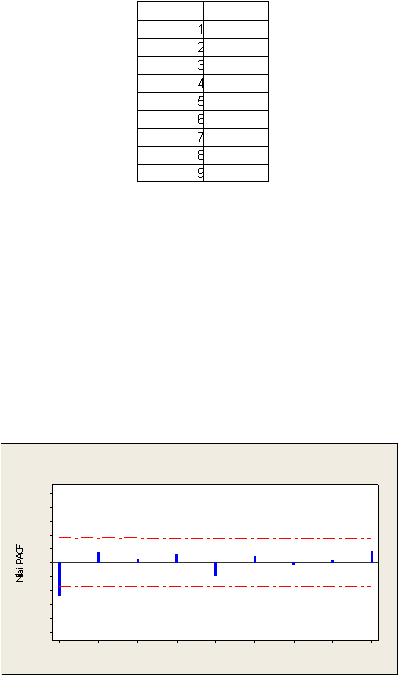
dalam selang kepercayaan, akan
diperoleh hasil seperti pada gambar 5.1.
A
uto co rrelation
Functio n
(A C F)
(dengan selang kepercay aan 95% )
1.0
0.8
0.6
0.4
0.2
0.0
-0.2
-0.4
-0.6
-0.8
-1.0
1
2
3
4
5
6
Lag
7
8
9
Gambar 5.1 Plot Nilai ACF Terhadap Selang Kepercayaan 95%
Dari gambar 5.1 tersebut, terlihat bahwa hanya lag 1 yang berada
di luar selang kepercayaan, sehingga dapat ditentukan bahwa nilai q
sebagai orde dari Moving Average (MA) bernilai 1.
5.2.3.2
Perhitungan Autokorelasi Parsial (PACF)
Dengan
menggunakan
persamaan
3.2.4.2.6,
3.2.4.2.7,
3.2.4.2.8,
3.2.4.2.9, pada data tabel 5.1, akan diperoleh nilai PACF dari lag 1 hingga
9 seperti ditunjukkan oleh tabel 5.3.
|
 47
Tabel 5.3 Nilai PACF
Lag
PACF1
-0.46501
0.145643
0.055788
0.11292
-0.17882
0.085146
-0.02966
0.023616
0.163738
Jika dibuat selang kepercayaan 95% (
a
=
5%) untuk nilai PACF
menggunakan persamaan 3.2.4.2.10, dengan nilai Z adalah 1.96 dan besar n
= 35, akan didapatkan selang kepercayaan berikut:
-
0.3313 = PACF (k ) = 0.3313
Dengan membandingkan nilai PACF pada tabel 5.3 dengan selang
kepercayaan di atas, akan diperoleh hasil seperti pada gambar 5.2.
P
artial A uto co rrelatio n Functio n (P A
C
F)
(
de nga n
s
e a ng
la ng
kepe rca
y
a
a
n
95% )
1.0
0.8
0.6
0.4
0.2
0.0
-0.2
-0.4
-0.6
-0.8
-1.0
1
2
3
4
5
6
7
8
9
La g
Gambar 5.2 Plot Nilai PACF Terhadap Selang Kepercayaan 95%
|
 48
Dari gambar 5.2 terlihat bahwa hanya nilai PACF pada lag 1 yang
berada
di
luar
selang
kepercayaan.
Hal
ini
menunjukkan
bahwa
nilai
p,
yang merupakan orde dari Autoregressive (AR), bernilai 1.
5.2.3.3
Identifikasi Model
Dari hasil perhitungan ACF dan
PACF di bagian sebelumnya,
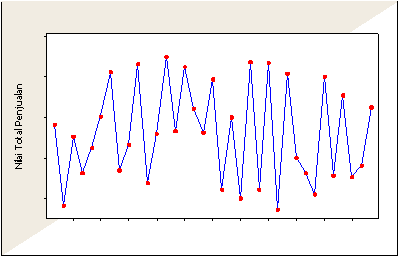
didapat nilai p = 1, dan q = 1. Sementara untuk nilai d, yang menunjukkan
orde pembeda, dianggap sama dengan 0, karena bentuk plot datanya cukup
stasioner
(gambar
5.3)
dan
dari
hasil
ACF
setelah
lag
ke-1, tidak
didapatkan
lagi
nilai
ACF
yang
berada
diluar
selang kepercayaan
seperti
dapat dilihat pada gambar 5.1. Sehingga model ARIMA yang didapatkan
adalah
model ARIMA(1,0,1) atau
model ARMA(1,1). Seperti persamaan
3.2.7.5.1, diperoleh bentuk persamaannya sebagai berikut:
Y
t
=
f
1
Y
t
-1
+
e
t
-
?
1
e
t
-1
(5.2.3.3.1)
Plot Deret Waktu dari T abel 5.1
70
65
60
55
50
3
6
9
12
15
18
21
24
27
Bulan
30
33
Gambar 5.3 Plot Deret Waktu dari Tabel 5.1
|
 49
5.2.3.4
Estimasi Parameter
f
1
dan
?
1
dan Diagnosis Model
Dengan
iterasi
menggunakan
persamaan
5.2.3.3.1,
untuk
menentukan
nilai
parameternya,
didapatkan
nilai
parameter
f
1
yang
optimal adalah
-0.86 dan
nilai
parameter
?
1
yang
optimal
adalah
-0.17,
sehingga persamaan 5.2.3.3.1 menjadi:
Y
t
=
?
+
(-0.86)Y
t
-1
+
e
t
-
(-0.17)e
t
-1
(5.2.3.4.1)
,
dengan t merupakan periode peramalan dan
?
merupakan konstanta yang
didapat
dari
_
?
=
Y 1 -
(1 -
f
1
)
=
58.077(1-(-0.86))
=
108.023,
dengan
memasukkan nilai
?
, persamaan 5.2.3.4.1 menjadi:
Y
t
=
108.023 + (-0.86)Y
t
-1
+
e
t
-
(-0.17)e
t
-1
(5.2.3.4.2)
Dari
hasil
peramalan
periode berjalan
menggunakan
model
5.2.3.4.1, didapatkan nilai
MAPE sebesar
7.477
dan
nilai
MSD
sebesar
32.741.
Untuk
melakukan
pengecekan
model,
diperlukan
nilai
autokorelasi sisaan seperti didapat pada tabel 5.4.
Tabel 5.4 Nilai ACF residual
ACF of Residuals
Lag
Value
-0.47
0.326
-0.16
0.17435
-0.256
0.2614
-0.2362
0.18172
0.01611
|
 50
Diagnosis
model
dilakukan dengan menggunakan nilai
autokorelasi sisaan untuk menentukan range dari suatu autokorelasi sisaan.
Dengan menggunakan persamaan 3.2.5.1, dimana akan didapat hasil seperti
pada tabel 5.5.
Tabel 5.5 Range dari ACF Residual
Selang ACF of Residuals
Lag
Min
max
-0.11716
0.558962
-0.23179
0.444338
-0.31246
0.363662
-0.30766
0.36846
-0.27253
0.403598
-0.26973
0.406392
-0.28227
0.393852
-0.30504
0.371084
-0.3378
0.338321
Dari nilai pada tabel 5.5, nilai nol berada pada selang antara nilai
minimum
dan
maksimum di
semua
time-lag,
sehingga
dapat
dikatakan
model yang telah diperoleh cukup sesuai untuk digunakan dalam
peramalan.
5.2.3.5
Model Peramalan ARIMA(1,0,1) atau ARMA(1,1)
Persamaan 5.2.3.4.1 merupakan model peramalan untuk periode
ke-t, sehingga untuk meramalkan periode ke-36, modelnya menjadi:
Y
36
=
108.023 + (-0.86)Y
36-1
+
e
36
-
(-0.17)e
36-1
(5.2.3.5.1)
Dan untuk periode selanjutnya digunakan persamaan
Y
35+
n
=
108.023 + (-0.86)Y
35+
n
-1
+
e
35+
n
-
(-0.17)e
35+
n
-1
(5.2.3.5.2)
|
|
51
,dimana nilai e untuk periode peramalan 35+n bernilai
nol, dan e3
5+n-1
juga
bernilai nol karena data tidak ada data aktual pada periode selanjutnya
setelah periode ke-35, sehingga galat/errornya tidak dapat dicari.
5.3
Implementasi
5.3.1
Spesifikasi Rancangan
5.3.1.1 Spesifikasi Perangkat Lunak
Spesifikasi perangkat
lunak
yang diperlukan
untuk
menjalankan
program aplikasi ini adalah sebagai berikut:
o
Sistem Operasi (Operating System): Windows XP
o
Apache Tomcat 4.1
o
Java2SE, Development Kit v5.0.
o
Java2SE, Runtime Environment v5.0
o
Web Browser, seperti:IE, Opera, dll.
5.3.2.1 Spesifikasi Perangkat Keras
Sedangkan
spesifikasi
perangkat
keras
yang
digunakan
pada
waktu implementasi program ini adalah sebagai berikut:
o
CPU Pentium IV 2,3 GHz
o
RAM 512 MB DDR.
o
Hard disk 80 GB.
o
Monitor 17 inci dengan resolusi 1024 x 768 pixels.
|
|
52
5.3.2
Instalasi Program
Langkah-langkah instalasi yang diperlukan untuk menjalankan program
aplikasi ini adalah sebagai berikut:
1. Lakukan instalasi Java Development Kit (JDK) dan Java Runtime Environment
(JRE) sesuai dengan petunjuk pada setup.
2. Lakukan setting environment variables pada System Properties windows pada
tab Advanced.
3. Pada bagian system variables, klik tombol New, lalu ketikkan JAVA_HOME
pada
variable name, dan lokasi instalasi jdk, misal: C:\Program
Files\Java\jdk.1.5.0_02 pada variable value. Lalu klik tombol OK.
4.
Ulangi langkah 3, tetapi ketikkan CLASSPATH pada
variable name, dan
ketikkan .; pada variable value.
5. Ulangi
langkah
3,
tetapi ketikkan
PATH pada variable name,
dan
ketikkan
%JAVA_HOME% pada variable value.
6. Copy-paste
Apache
Tomcat 4.1 di
mana saja (biasanya di C:\Program Files),
lalu masukkan file ekstensi java dan class (file java yang telah di compile) ke
dalam
folder C:\Program Files\Apache Group\Tomcat
4.1\common\classes\forecasting,
lalu
masukkan
file
jsp
ke
dalam
folder
C:\Program Files\Apache Group\Tomcat 4.1\webapps\ROOT\forecasting.
7. Jalankan
Tomcat
startup
yang berada pada
folder
C:\Program
Files\Apache
Group\Tomcat 4.1\bin.
8.
Jalankan aplikasi web browser,
misalkan
IE,
lalu pada
address
bar ketikkan
http://localhost/forecasting dan enter.
|