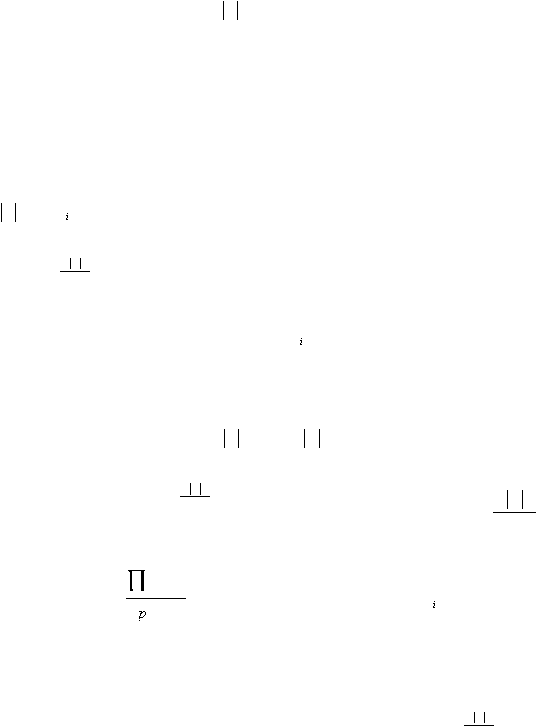
60
i
p
p
Jika
faktorisasi prima dari G
tidak diketahui,
maka
tidak
mudah
untuk
mencari
order g. Khususnya pada algoritma
ElGamal, order
grup dan
faktorisasi primanya telah
diketahui.
Teorema 2.1.4.16. (Buchmann, 2000)
Diketahui
grup
G
dan
faktorisasi
prima
n
G
=
?
p
e( p
i
)
. Jika
g
?
G
dan
f
(
p
i
)
adalah bilangan bulat
terbesar sedemikian
i
=1
hingga
g
p
i
G
f
(
p )
i )
=
1, 1 = i =
n
,
maka:
n
order g =
?
p
e( p
i
)- f ( p
i
)
.
i
=1
Bukti:
Misalkan faktorisasi prima dari G
adalah
n
G
=
?
p
e p
( p
i
)
. Menggunakan
Teorema
i
=1
2.1.4.10 diperoleh bahwa
g
p
i
G
f
(
p
i
)
=
1
jika dan hanya jika order g
membagi
G
f
(
p
i
)
i
atau
n
e( p
i
)
i
n
order
g
membagi
i
=1
.
Akibatnya
order
g
membagi
f
(
p
i
)
i
?
i
=1
p
e p
( p
i
)- f ( p
i
)
.
Diperoleh
n
bahwa order g =
?
p
x
(
p
i
)
dengan
0
=
x( p
)
=
e( p
)
-
f ( p
)
,
untuk setiap
p
,
1
=
i
=
n
.
i
i
=1
i
i
i
i
Karena
f
(
p
i
)
adalah bilangan bulat terbesar sedemikian hingga
g
p
i
G
f
(
p
i
)
=
1
maka
x( p
i
)
=
e( p
i
)
-
f ( p
i
)
, untuk setiap
p
i
,
1
=
i
=
n
. Dengan demikian diperoleh bahwa:
n
n
order
g
=
?
p
x
(
p
i
)
=
?
p
e p
( p
i
)- f ( p
i
)
.
i
i
=1
i
i
=1