11
mempertimbangkan
bahwa
semua
titik-titik
(x,
y)
mendefinisikan
semua
garis
yang sama dalam ruang (A, B) tersebut. Di
mana, jika himpunan titik-titik
kolinear {(x
i
, y
i
)} mendefinisikan garis (A, B), maka
Ay
i
+
Bx
i
+
1
=
0
…………………………………………...(2.3)
Persamaan
ini
dapat
dilihat
sebagai
sebuah
sistem
dan
dapat
dituliskan
secara sederhana dalam parameter kartesius sebagai
c
=
-
x
i
m
+
y
i
……………………………………………….(2.4)
Maka
untuk
menemukan
garisnya
kita
harus
menemukan
nilai-nilai
dari
parameter
(m,
c)
(atau
(A,
B)
dalam
bentuk
yang
homogen)
yang
memenuhi
persamaan 2.4 (atau 2.3).
Hubungan
antara
sebuah
titik
(x
i
,
y
i
)
dalam
sebuah
gambar
dan
garis
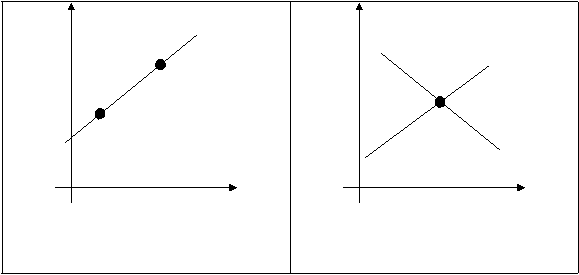
dalam persamaan 2.1 sampai 2.4 digambarkan dalam grafik di bawah ini.
y
y
(x
i
, y
i)
(x
j
, y
j
)
(A, B)
x
x
(a)Gambar yang memuat sebuah garis
(b)Garis-garis dalam ruang ganda
Gambar 2.2. Ilustrasi Transformasi Hough untuk garis