Skew
coefficient
C
s
or C
w
Return Period in Years
2
5
10
25
50
100
200
Exceedence Probability
0.50
0.20
0.10
0.04
0.02
0.01
0.005
-2.1
0.319
0.765
0.869
0.923
0.939
0.946
0.949
-2.2
0.330
0.752
0.844
0.888
0.900
0.905
0.907
-2.3
0.341
0.739
0.819
0.855
0.864
0.867
0.869
-2.4
0.351
0.725
0.795
0.823
0.830
0.832
0.833
-2.5
0.360
0.711
0.771
0.793
0.798
0.799
0.800
-2.6
0.368
0.696
0.747
0.764
0.768
0.769
0.769
-2.7
0.376
0.681
0.724
0.738
0.740
0.740
0.741
-2.8
0.384
0.666
0.702
0.712
0.714
0.714
0.714
-2.9
0.390
0.651
0.681
0.683
0.689
0.690
0.690
-3.0
0.396
0.636
0.666
0.666
0.666
0.667
0.667
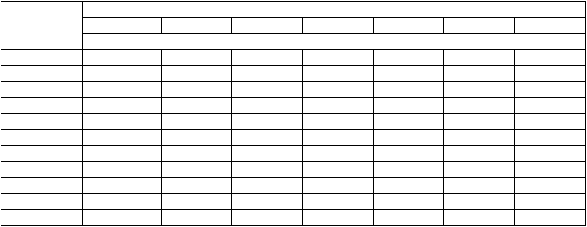
Tabel 2.6. Nilai KT Untuk Distribusi Pearson III ( Lanjutan )
Sumber : Hidrologi Terapan, Bambang Triatmodjo, 2000
Distribusi log
Pearson
III
digunakan
apabila
parameter statistik
C
s
dan
C
k
mempunyai nilai
selain dari
parameter
statistik
untuk distribusi
yang
lain
(
normal,
log
normal,
Gumbel
).
Penggunaan metode
log
Pearson
III
dilakukan dengan
menggunakan
langkah – langkah berikut ini.
a.
Data maksimum tahunan disusun dalam tabel
b.
Hitung nilai logaritma dari data tersebut dengan transformasi
y
i
=
ln x
i
atau
y
i
=
log x
i
c.
Hitung nilai rerata ??, deviasi standar s
y
, koefisien kemencengan C
sy
dari nilai logaritma y
i
.
d.
Dihitung
nilai y
j
untuk
berbagai
priode
ulang yang dikehendaki
dengan
menggunakan
persamaan 2.47
e.
Hitung x
T
untuk setiap periode ulang dengan menghitung nilai anti-lognya :
x
T
=arc ln y atau
x
T
=arc ln y
Pada setiap perhitungan distribusi diatas
memiliki persyaratan – persyaratan yang
harus di penuhi sebagai dasar dalam pemilihan penggunan
metode distribusi.
Persyaratan tersebut dapat dilihat pada tabel 2.5. berikut ini.
Tabel 2.7. Persyaratan Masing – Masing Distribusi