15
2.2.2
Notasi Big-O
Dalam teori
penghitungan
kompleksitas,
notasi
Big-O digunakan
untuk
menggambarkan
bagaimana ukuran
data
input
mempengaruhi
kecepatan
dan
penggunaan
memori.
Notasi
Big-O
juga
digunakan
pada matematika untuk
menghasilkan
estimasi
yang
mirip.
Notasi
Big-O
disebut
juga
notasi
Bachman-Landau
atau notasi Asimtotis.
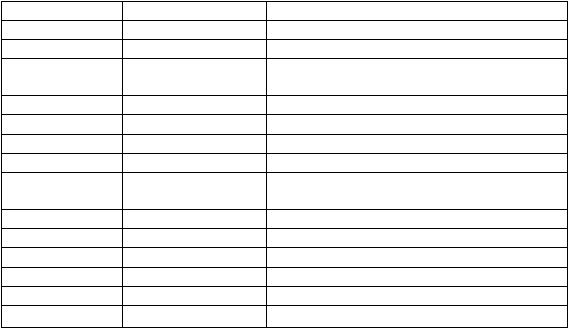
Tabel 2.2 Notasi Big-O
Notasi
Nama
Contoh
O(1)
Konstan
Menentukan genap / ganjil suatu bilangan.
O(a(n))
Ackermann invers
O(log* n)
Logaritmik
beriterasi
Hopcroft
and
Ullman
search
dengan
menggunakan disjoint set.
O(log n)
Logaritmik
Binary Search
O((log n)©)
Polilogaritmik
Test Primalitas AKS
O(n©) ;0 < C < 1
Akar
Pencarian pada KD-Tree
O(n)
Linear
Sequencial Search
O(n log n)
Linearitmik
dan
Loglinear
Heapsort, Fast Fourier Transform
O(n²)
Kuadratik
Insertion Sort
O(n©)
Polinomial
Algoritma Floyd-Warshall
O(c
n
)
Eksponensial
Travelling Sales Problem
O(n!)
Faktorial
Brute Force
O(n
n
)
Eksponensial n
(
)
Eksponensial ganda
Notasi
Big-O
sangat
berguna dalam
analisis
algoritma
dalam
hal
efisiensi.
Contohnya,
waktu
dan
jumlah
langkah
yang dibutuhkan
untuk
menyelesaikan
suatu
persoalan dengan ukuran data n dapat dihitung dengan cara berikut:
(
)