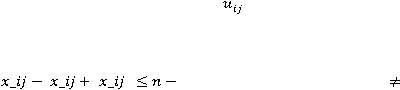
49
disesuaikan untuk mengatur satu variabel dari subtour
sama dengan 0
(melihat bahwa semua variabel yang berhubungan dengan subtour sama
dengan 1). Solusi dari hasil assignment problem
bisa saja dapat
menghasilkan tour
atau perjalanan tetapi bisa juga tidak. Jika
menghasilkan tour, kita dapat menggunakannya sebagai nilai objektif
sebagai nilai batas atas (upper bound) pada minimum panjang perjalanan.
Jika tidak, selanjutnya pencabangan dibutuhkan, membuat cabang-cabang
sebanyak jumlah variabel pada setiap subtour. (Taha, 2007, p386)
3.
Algoritma Cutting-Plane
Algoritma ini dicetuskan untuk menambah satu batasan pada assignment
problem untuk mencegah pembentukan subtour. Batasan yang
ditambahkan dapat didefenisikan sebagai berikut. Dalam situasi n-kota,
menghubungkan variabel yang kontinu
(
=0) dengah kota
-kota 2,3, . . .
, dan n. Selanjutnya, didefenisikan kebutuhan jumlah batasan tambahan
1, i = 2,3 . . . ,n; j = 2,3, . . ., n : i
j
Batasan ini, ketika ditambahkan pada model assignment, secara otomatis
akan menghapus sema solusi subtour. (Taha, 2007, p386)