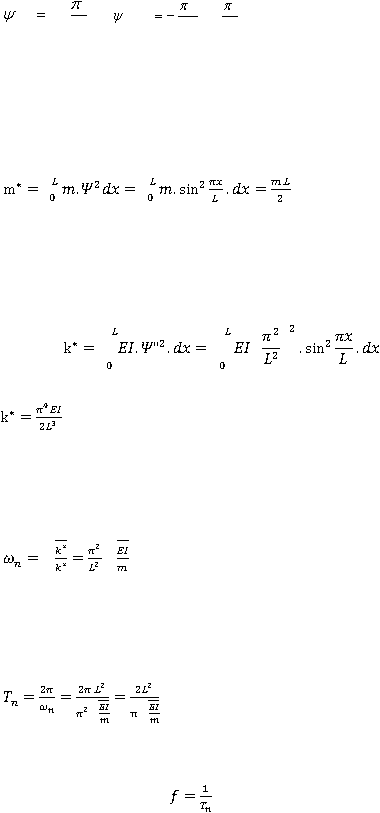
45
L
x
x)
sin
(
?›
L
x
L²
x)
sin
(
"
2
................................. (2.19)
b.
Menurunkan Rumus Frekuensi Alamiah
Dari shape functiondiatas maka didapatkan generalized mass (massa tergeneralisasi)
adalah sebagai berikut
ì
ì
...................... (2.20)
Dengan menggunakam double differential
dari shape functionmaka generalized
stiffness (kekakuan tergeneralisasi) adalah sebagai berikut:
±
±
F
G
..............................................................................
(2.21)
Dengan menggunakan generalized massdan generalized stiffness yang telah didapat
dari persamaan sebelumnya maka natural circular frequency adalah sebagai berikut:
§
§
.............................................................. (2.22)
Dengan memasukan persamaan dari natural circular frequencymaka didapatkan
persamaan natural period adalah sebagai berikut:
§
§
....................................................... (2.23)
Karena frekuensi alamiah adalah
maka, persamaan frekuensi alamiah untuk
struktur jembatan adalah sebagai berikut: