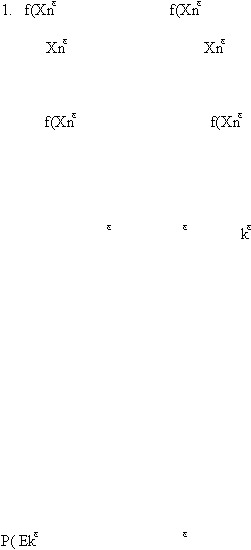
20
2.4.2.
Sifat Umum
Sifat umum dari proses Markov adalah :
Xn-1,……,X1) =
Xn-1)
2. E{
Xn-1,……,X1} = E{
Xn-1}
3. Proses Markov juga Markov bila waktu dibalik :
Xn+1,……,Xn+k) =
Xn+1)
4. Bila
keadaan
sekarang
diketahui,
masa
lalu
independen
dengan
masa
akan
datang, bila k<m<n maka :
f(Xn,XkXm) = f(XnXm) f(X
Xm)
2.4.3. Definisi Rantai Markov
Diberikan sebuah himpunan N dengan keadaaan E = { E1,E2, …, EN} dan
rantai keadaan itu :
Ej1, Ej2, Ej3,……EjN
Rantai tersebut adalah rantai Markov bila :
Ej1Ej2…..Eji ) = P( EkEji )
2.4.3.1 Rantai Markov Diskret
Rantai Markov
waktu diskret adalah proses
Markov
Xn
yang
mempunyai
keadaan (state) terbatas ai, dicirikan dalam bentuk probabilitas keadaannya :
Pi[n] = P{Xn = ai} i = 1,2,…