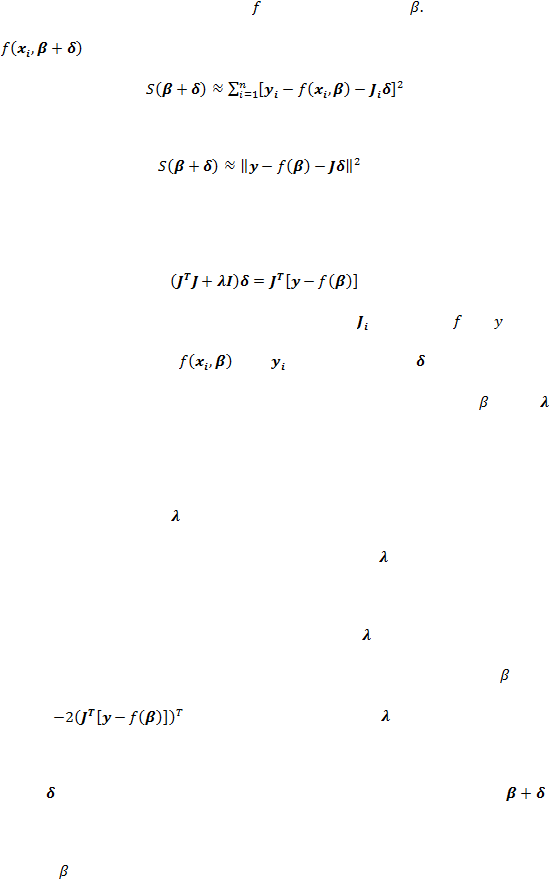
11
adalah gradient (vektor baris) dari
terhadap parameter
Aproksimasi dari
akan menghasilkan,
(2.7)
atau dalam notasi vektor menjadi,
(2.8)
Berdasarkan Levenberg (1944) dan Marquardt (1963), Metode Levenberg-
Marquardt memodifikasi step dari Gauss-Newton menjadi
(2.9)
dimana J adalah matriks jacobian yang memiliki baris
dan dimana
dan
adalah
vektor dengan komponen
dan
sebanyak i. Nilai
adalah nilai yang
memberikan arah turun (descent direction) terhadap vektor parameter
. Nilai
merupakan damping parameter yang tidak boleh bernilai negatif dan akan
disesuaikan di setiap iterasi.
Damping parameter,
, akan disesuaikan di setiap iterasi. Jika penurunan S
sangatlah drastis atau cepat, dapat menggunakan nilai
yang kecil, yang akan
membuat metode ini menjadi hampir sama dengan metode Gauss-Newton, dimana
iterasi akan memberikan hasil residual yang kecil. Nilai
dapat diperbesar yang akan
memberikan arah penurunan terhadap gradien dengan gradien S terhadap
sama
dengan
. Oleh karena itu, untuk nilai
yang besar, tahap-tahap
akan dilakukan secara aproksimasi ke arah gradien. Iterasi berhenti jika banyaknya
tahap,
, atau pengurangan Sum of Squares dari vektor parameter terakhir,
,
sudah dibawah limit yang telah ditentukan. Berdasarkan Monahan (2011), parameter
terakhir,
, menjadi solusi dari metode Levenberg-Marquardt dapat dituliskan dalam
persamaan (2.17).