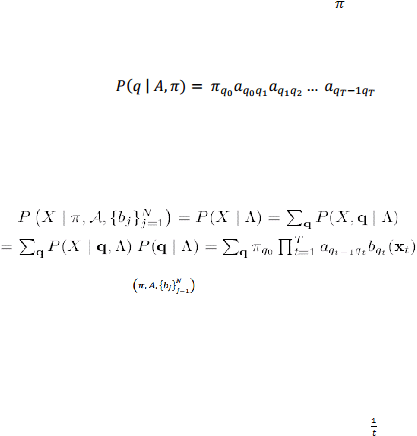
23
Pemodelan HMM adalah pemodelan statistik sinyal suara yang
populer dan bagus.
Diberikan
suatu
ucapan,
misalkan
X = (x1,
x2,
… , x
T
)
menjadi fitur
urutan vektor terekstraksi dari gelombang suara, dimana x
T
menunjukkan suatu pengukuran vektor jangka pendek dan secara
konvensional sebuah vektor cepstral.
Suatu permintaan awal N-state rantai Markov diperintah oleh suatu
transisi state peluang matriks
A=
{a
ij
}
, dimana
a
ij
adalah peluang pembuatan
transisi dari state I kestate j. Asumsikan bahwa pada t=0, state pada sistem q
0
dikhususkan oleh suatu
inisial state dengan peluang
i
= P(q
0
=i). Lalu,
untuk
setiap
urutan state q = (q1, q2,… ,q
T
), peluang q yang dihasilkan dari rantai
Markov yaitu:
(2.10)
Anggap
pada
sistem,
ketika
distate
q
T
,
keluarkan
observasi
x
T
menurut
distribusi b
qt
( X
t
) =P(X
t
| q
t
), q
t
= 1,2, …, N. HMM digunakan
sebagai distribusi
ungkapan suara X lalu didefinisikan sebagai:
(2.11)
Dimana
? =
adalah himpunan parameter untuk model.
Seperti pada persamaan 2.5,
{b
qt
}
mendefinisikan distribusi untuk observasi
jangka pendek dan
A
mencirikan sifat
dan
hubungan
diantara
state
yang
berbeda dari proses penghasilan suara. Secara
umum, N
(jumlah
total state)
lebih
kecil
dari
T
(waktu selama
pengucapan
suara).
Urutan
state
q
menunjukkan derajat stabilitas tertentu diantara adjacent q
S.
Tiga
masalah dasar
dalam
HMM
yang
harus
dikaji
ulang
yaitu
masalah evaluasi, masalah decoding dan
masalah estimasi. Masalah evaluasi
adalah
memperkirakan peluang
P(X|
?
)
dari pengamatan
fitur suara urutan
vector X yang diberikan
Hidden
Markov
Model.
Masalah
decoding
yaitu
untuk
menemukan urutan state terbaik q yang optimal dari urutan fitur suara
X. Karena state dalam HMM terhubung
kekata
dan
kelas
kata,
urutan
kata
dalam
pengucapan suara
dapat
diidentifikasikan
dengan
menelusuri
label
kata pada
urutan state q.Masalah
yang ketiga
yaitu estimasi
yang diperlukan
untuk memperkirakan parameter HMM ? dari
himpunan
sampel
yang sudah