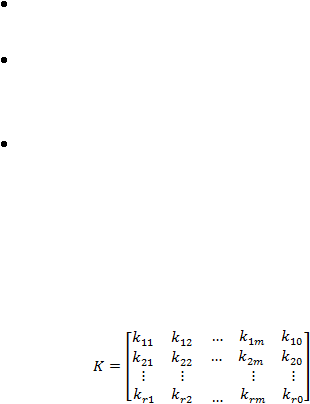
37
adalah m, dan variabel output biasanya 1. Pada metode ini, akan diperoleh
kumpulan aturan yang berbentuk :
[R1]
IF (x1 is A
11
)
o
(x2
is A
12
)
o
...
o
(x
n
is A
1m
) THEN
(z=k
11
x1+...+k
1m
x
m
+k
10
);
[R2]
IF (x1 is A
21
)
o
(x2
is A
22
)
o
...
o
(x
n
is A
2m
) THEN
(z=k
21
x1+...+k
2m
x
m
+k
20
);
...
[Rr]
IF (x1 is A
1m
)
o
(x2
is A
2m
)
o
...
o
(x
n
is A
rm
) THEN
(z=k
r1
x1+...+k
rm
x
m
+k
r0
);
Dengan :
A
ij
adalah himpunan fuzzy
aturan ke-i variabel ke-j sebagai
anteseden,
k
ij
adalah koefisien persamaan output
fuzzy
aturan ke-i variabel
ke-j (i=1,2,...,r; j=1,2,...,m), dan k
i0
adalah konstanta persamaan
output fuzzy aturan ke-i;
tanda
o
menunjukkan operator yang digunakan dalam anteseden.
Jumlah aturan = r yang terbentuk, sama dengan jumlah
clusteryang terbentuk. Misalkan setelah melakukan clustering
diperoleh 5 pusat cluster, maka nantinya dalam FIS juga akan
memiliki sebanyak 5 buah aturan.
Untuk mempermudah komputasi, matriks K yang berukuran r
x (m+1):
disusun menjadi satu vektor k:
k = [k
11
k
12
... k
1m
k
10
k
21
k
22
... k
2m
k
20
... k
r1
k
r2
... k
rm
k
r0
]
T
yang berukuran r*(m+1).
Karena kita memiliki n buah titik data, tentu saja kita dapat
mencari derajat keanggotaan setiap titik data i dalam setiap cluster k
dengan menggunakan fungsi Gauss.
Berbeda dengan derajat keanggotaan pada fuzzy
substractive
clustering, pada bagian ini derajat keanggotaan hanya melibatkan