Fs = ku = gaya luar kompo nen kekaku an terhada
perpindahan gerakan tanah.
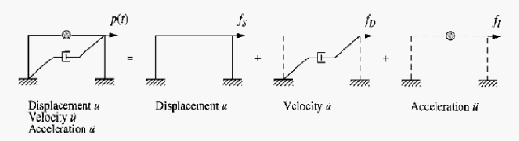
Gambar 2.15 Modelisasi Kesetimbangan SDOF Dinamik
P(t) = f1 + fd +fs ......... ......................... ......................... ....
(2.21)
Atau dapat juga ditulis,
(2.22)
Massa keseluruhan (m) dari sistem ini dicakup dalam balok tegar terhadap
percepatan gerakan ( ). Tahanan elastik terhadap perpindahan diberikan oleh pegas
tanpa bobot dengan kekakuan (k) terh adap perpindahan gerakan (u), sedangkan
mekanisme kehilangan energi (eneg y loss) digambarkan oleh peredam (c) terhadap
kecepatan gerakan ( ). Mekanisme pembebanan luar yang menimbulkan respon
dinamik pada sistem dengan bentuk p(t) yang berubah menurut waktu.
2.8.3 Sistem SDOF Dengan Getaran Bebas
Sistem SDOF getaran bebas terbagi menjadi 2 yang akan dibahas lebih
lanjut dalam subbab berikut ini.
2.8.3.1 Geta ran Bebas Tanpa Redaman
Struktur hanya mengalami getaran karen a beban sendiri tanpa adanya beban
luar yang bekerja dan tidak mengalami efek redaman dimana c=0. Sehingga
persamaan khusus SDOF getaran bebas tanpa redaman dapat ditulis sebagai berikut.
............................................................................... (2.23)
Dengan solusi umum persamaan gerak yang terjadi adalah,
................................................ (2.24)
dimana adalah frekuensi alamiah sudut,