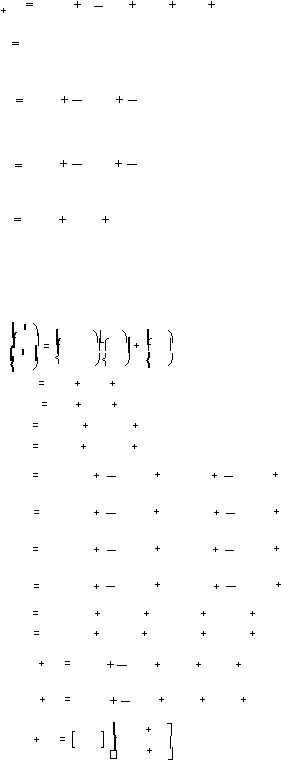
17
lainnya (Canale et al., 1994, pp233-248). Persamaan
umumnya adalah
sebagai berikut:
Rumus dari metode runge kutta orde 4 :
y
y
1
(k
2k2
2k3
k
)
h.................(2
14)
i
1
i
6
1
4
Dengan
k1
f (x , y
i , y
i
)
k
f
(
x
1
h,
y
1
k
h)
2
i
2
i
2
1
k
f ( x
1
h,
y
1
k
h)
3
i
2
i
2
2
k
4
f ( x
i
h,
y
i
k3
h)
Berikut
ini
merupakan
rungge
kutta
orde
4
yang
digunakan
untuk
mencari persamaan diferensial orde 2 :
x1
a
b
x1
b1
c
u
d
x
b2
x
2
2
x1 (i )
ax
1
bx
2
b1
u x
2
(i )
cx
1
dx 2
b2
u
k
11
ax
1
(i )
bx
2
(i )
b1
u
k
12
cx
1
(i )
dx 2 (i )
b2
u
k
(
a
(
x 1
(i )
1
h.k
)
b ( x
(i )
1
h.k
)
b u )
21
2
11
2
2
12
1
k
(c ( x
(i )
1
h.k
)
d ( x
(i )
1
h.k
)
b
u
)
22
1
2
11
2
2
12
2
k
(
a
(
x
(i )
1
h.k
)
b ( x
(i )
1
h.k
)
b u )
31
1
2
21
2
2
22
1
k
(c ( x
(i )
1
h.k
)
d ( x
(i )
1
h.k
)
b
u
)
32
1
2
21
2
2
22
2
k
41
(
a
(
x1 (i )
h.k
31
)
b ( x
2
(i )
h.k
32
)
b1
u
)
k
42
(c ( x1 (i )
h.k
31
)
d ( x
2
(i )
h.k
32
)
b2
u
)
h
x1 (i
1)
x1 (i )
x
2
(i
1)
x
2
(i )
(
k
11
2
k
21
2
k
31
k
41
)
6
h
(
k
12
2
k
22
2
k
32
k
42
)
6
x
(i
1)
y
(i
1)
1
0
1
x
2
(i
1)