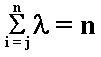
Bila
matriks
ini
dikaitkan dengan
vector
kolom
W=
(W1,
W2,….,Wn),
maka diperoleh hubungan:
AW = nW………….…..(1)
Bila
matriks
A
diketahui dan
ingin
diperoleh nilai
W,
maka
dapat
diselesaikan melalui persamaan berikut:
[ A-nI ] W = 0………….(2)
dimana I adalah matriks Identitas.
Persamaan
(2)
ini
dapat
menghasilkan solusi
yang
tidak
nol
bila
(jika
dan
hanya jika) n merupakan eigenvalue dari A dan W adalah eigenvektor-nya.
Setelah
eigenvalue
matriks
perbandingan
A
tersebut
diperoleh,
misalnya
?1, ?2,…..,?n,
dan berdasarkan
matriks A
yang
mempunyai keunikan,
yaitu aij =
I dengan I = 1,2,….,n, maka:
Disini
semua
eigenvalue bernilai
nol,
kecuali
satu
yang
tidak
nol,
yaitu
eigenvalue
maksimum. Kemudian
jika
penilaian
yang dilakukan konsisten,
maka
akan diperoleh eigenvalue maksimum pada persamaan:
AW = ?
maks W
Selanjutnya persamaan (2) dapat diubah menjadi:
[ A - ? maks I ] W = 0 …………...(3)