21
Dengan
membtTikan
batasan
(scpcrti
3
<
X1
<
4), Kita
akan
menghasilkan
soiusi
yang
optimal yang
memenub
persyarata..11
untuk
batasan
integer.
Pembagian
atau
pcmbatasan
sepe1ii
ini
n1erupakan
konsep
dari
branching
daiam algorima
Branch
and
Bound dcngan
X
1
menJadi
va;:iabel
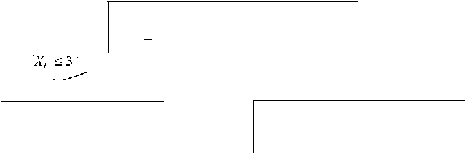
branching. Solusi yang diperoleh seperti tarnpak pada
gambar 2.L
PLO
X
1
,
3,75; X2
-1,25; L;..;;23,75
X,24
1
l'L2
II
x,-3;J,
2;Z 23
x,-
4;
x,-
0,83 ; 7
=
23,33
.
I3atas
Bawah/
01-ver
Bound
(optn:rum)
'--
-
· ··..
Gambar 2.1. Sohxsi l
Untuk Cm:toh Soaf
2.H.
Sobsi yang dihasilkan pada P Ll
memenuhi persyaratan integer untuk X1 dan
X1
dan
nilai Z
dalam PLl
menjadi
batas
bawah
(lower bound). Selanjutnya
diadakan
pembatasan
pada
PL2
menjadi
beherapa
submasalah
(suhprohlem). Jika
submasalah
tersebut
menghasilkan sohJsi
integer yang
lebi.h besar
cari
batas
1aw.ah,
maka
hatas
bawah
han1s
diupdate.