22
x 3,75 ;x2
1,25
;Z 23,75
x,
/
------
----------
PLO
,4
I'L1
I
I'Ll
--
..
J
...
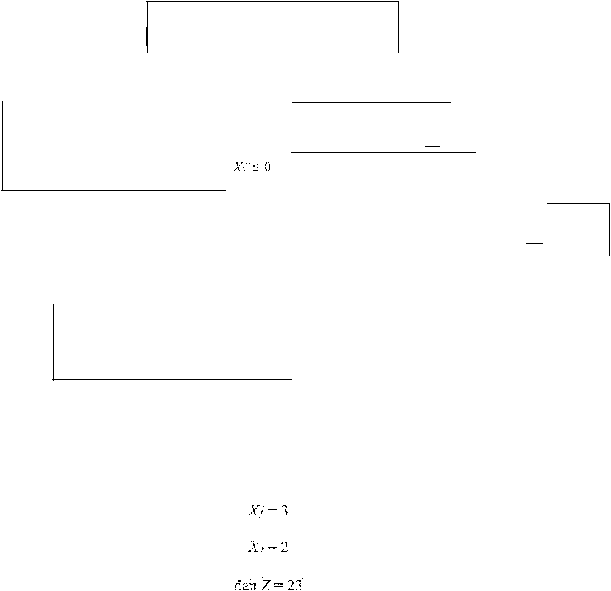
x1 =
3
;
x2 = 2;
z
=
23
' Xt
=
4;
x2 =
o,s3
-
?. :33
Batas Bmvah
I Tower Round
(optimum)
-
I'L3
I'L4
X
1 =
4,5; -¥2 =
.-¥2 =
0; Z- 22,5
Solusi
tida.kfeasibi';'
X
1
o4
''
PLS-
6
X1 =
4
;
Xi= 0
;
7:- 20
1
I
Solusi tidak feasible
Batas
Bawah
I
Lower Bound
Gambar 2.2. Sohrsi H
Untuk
Contoh Suai
2.8.
Dari
gamb.ar 2.2.,
Bat.as
bawah
untuk
PL5
lebih
kecil
dari
batas
bawah
untuk
PLl
sehi_ngga
solusi optimal ya.."'lg dipilih yaitu PLl
dengan nilai
Jadi
secara
umum,
Langkah - l<mgkah
pcnyclcsaian
algoritma
Branch
and Bound
untuk fungsi tujuan
rnaksimum adalah scbagai berikut
:
Langkah
1
:
(Pcmbatas2.::1).
Tentukan
nilai
Z
awal
=
-
untuk
fungsi
tujuan
optimum
pada
pemrograr:lS'11inear
integer.
Tentukan
i...,.
0.
Pilih
pcmrog.raman
linear
ke
t
(pl;).
Submasalah selanjutnya diperiksa.