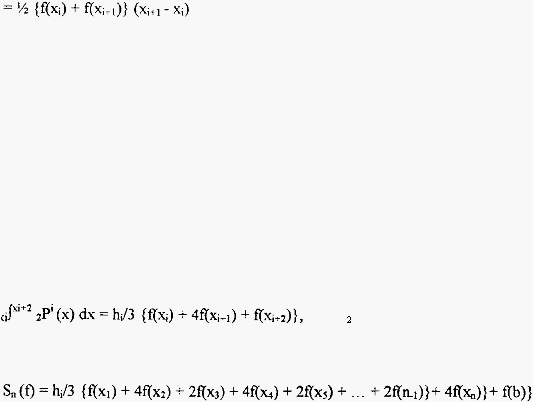
16
2.1.3.2
Aturan
Trapesium
Menurut
Djauhari
(1991,
p120),
Aturan
Trapesium
menghitung
suatu
1uasan
yang
terbentuk
di bawah
suatu
garis maupun kurva,
dengan
membagi
garis
atau
kurva
tersebut
ke
dalam
bagian-bagian
yang
membentuk
ataupun
hampir
membentuk
garis-
garis
lurus.
Integral
dari
garis-garis
lurus
itu
membentuk
luasan-luasan
trapesium.
Jumlah
dari
seluruh
luasan
trapesium
tersebut
adalah
pendekatan
terhadap
luas
dari
kurva yang dibentuk.
xifxi+l 2Pi (x)
dx = xJ
i+l {fTxi]
+
f
[x;,
X;+I] (x- x;)
dx
_
- '\X
f
Y
)
xi
fxi+l
d
X
+
f
[
X;, X;+ I
]
xi
fxi+l
(
X
- i
Xi
)
d
X
=
t{x)
(xi+ I- x;)
+
f[x;, X;+I]. Y2(x-
xl
=
f{x)
(xi+I- x;)
+
{fl:xi+I)- t{x;)}/(xi+!-
x;) . Y2(x-
xi
n
I(g,) = Y2
r. h; {f{x;)
+
fl:Xi-I)}
i=l
2.1.3.3 Metode Simpson
Aturan
Simpson (Djauhari,
1991, p124)
mengatakan
harga
I(f)
J'
t{x) dx
didekati I(g2) yang sama dengan:
n
J'
g2 (x) dx
=
L
xiJxi-² 2Pi dx, x
di
interval [x, X;+
]
adalah:
i=l
sehingga