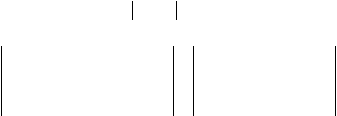
25
?
?
?
4
?
?
?
?
Dengan cara mengekspansi
?I -
A
=
0
, kita dapat mencari nilai eigen:
?
?
0
?
0
?
?
1
?
?
-
3
3
?
?
?
?
-
1
3
?
-
3
?
?
?
0
?
0
?
-
?
3
-
5
3
?
=
?
-
3
?
+
5
-
3
?
=
?
0
0
?
?
6
-
6
?
?
-
6
6
?
-
4
?
(? + 2)
2
(? - 4)
=
0
Maka, nilai eigen dari matriks A adalah -2 dan 4.
Sekarang kita akan mencari vektor eigen untuk matriks A.
?
v1
?
?
?
Misal
v
=
?
v2
?
adalah
vektor
eigen
untuk
matriks
A
yang
berkorespondensi
?
?
?
v3
?
dengan nilai eigen
?
=
-2 . Maka:
(
?I -
A
)
v
=
0
?
?
-
1
3
-
3
??
v1
?
?
0
?
?
??
?
?
?
?
-
3
?
+
5
-
3
??
v2
?
=
?
0
?
, dan untuk
?
=
-2 menjadi:
?
??
?
?
?
?
-
6
6
?
-
4
??
v3
?
?
0
?
?
-
3
3
-
3
??
v
?
?
0
?
?
-
3v1
+
3v2
-
3v
=
0
?
??
1
?
?
?
3
?
?
-
3
3
-
3
??
v2
?
=
?
0
?
,atau
?
-
3v1
+
3v2 - 3v3 = 0
?
??
?
?
?
?
?
-
6
6
-
6
??
v3
?
?
0
?
?
-
6v1
+
6v2 - 6v3 = 0
,atau
v1
-
v2 + v3 = 0 , atau
v1 = v2 - v3 .
Himpunan jawab dari sistem persamaan linear homogen di atas, adalah: