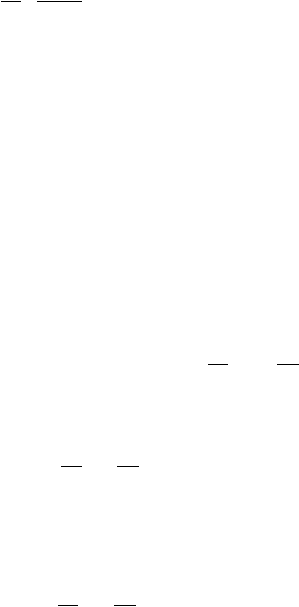
21
0
=
?F
-
d ?F
(2.6.9)
?f
dx ?f'
2.7 Metode Variasional
Penggunaan
simbol
variasional d yang
mempunyai
fungsi
yang
secara
analogi
sama
dengan
diferensial d pada
kalkulus
akan
lebih
mudah.
Misalkan
diberikan sebuah
fungsi F(x, y(x), y'(x)) , atau
lebih singkatnya
F(x, y, y') di
mana kita tetapkan x bernilai tetap, dapat kita nyatakan
?F = F(x, y(x) + e?(x), y'(x) + e?'(x)) - F(x, y(x), y' (x))
(2.7.1)
Dengan menggunakan deret Taylor
F(x, y + e?, y'+e?') = F(x, y, y') +
?F
e? + +
?F
e?'+...
(2.7.2)
?y
?y'
persamaan (2.6.1 ) dapat ditulis menjadi
?F
?F
?F =
?y
e? +
?y'
e?'+...
(2.7.3)
Jumlah
dari
bentuk
kedua
pertama
pada
bagian
kanan
pada
persamaan
(2.7.3) didenotasikan oleh
dF
dan disebut variasi dari F, misalnya
dF
dF
dF =
e? +
e?'
dy
dy'
(2.7.4)
Jika dalam hal tertentu F=y atau F=y’ pada persamaan (2.7.4), kita
akan
memperoleh
dy = e?,
dy'= e?'
(2.7.5)
sehingga persamaan (2.4.4) dapat ditulis menjadi