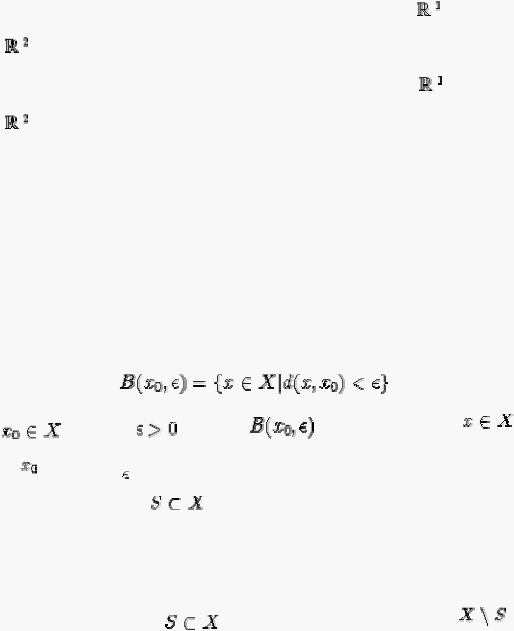
9
Pandangan dimensi euclidean mendapat sanggahan pada akhir abad ke-19 oleh dua
penemuan berikut:
•
Cantor set membuktikan adanya korespondensi satu-satu antara
(satu dimensi) dan
(dua dimensi).
•
Konstruksi
Peano
mengenai
pemetaan
yang
berkelanjutan
dari
(satu
dimensi)
ke
(dua dimensi).
Sanggahan ini menunjukkan bahwa pandangan mengenai dimensi belum cukup kuat.
Pada awal abad ke 20, ahli matematika menemukan definisi yang tepat mengenai dimensi.
Definisi ini disebut dimensi topologi.
Sebagai permulaan perlu dimengerti
mengenai open
set dan closed set. Dalam sebuah
ruang metrik X didefinisikan (Barnsley, 1994, p12):
Open ball:
sebuah open ball dalam X adalah sebuah subset dalam bentuk
Untuk
dan
radius
.
Artinya,
mengandung
semua
dengan
jarak dari
kurang dari
.
Open:
sebuah
subset
adalah
open
jika
merupakan
arbitrary
union
dari
open
balls dalam
X.
Artinya
tiap
titik
dalam
S
dikelilingi
oleh
open
ball
yang
seluruhnya
berada di dalam X.
Closed: sebuah subset
adalah closed jika komplemennya dalam X
adalah open.
Hal
ini
juga bisa digambarkan dengan
mengatakan bahwa titik
manapun
di dalam X yang merupakan limit dari deretan titik dalam S harus terkandung dalam S.