36
H
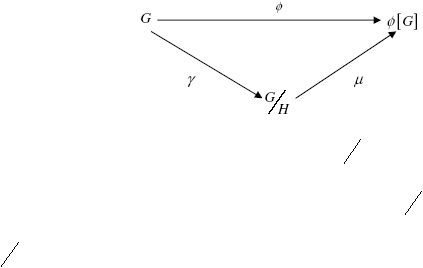
Gambar 2.3. Hubungan antara G,
G
H
dan f
[G]
Karena
terdapat
isomorfisma
antara
grup
faktor
G
H
G
?
f
[G].
D.
Gelanggang dan Lapangan
dan
f
[G]
, maka
Berikut
ini diperkenalkan suatu struktur aljabar
yang
lain,
yaitu
gelanggang dan
lapangan.
Serta
diberikan
beberapa
definisi
yang
berhubungan
dengan
gelanggang
dan
lapangan.
Definisi 2.1.3.12. (Fraleigh, 2000)
Suatu
gelanggang
(ring)
(R,+,·)
adalah
himpunan
R
tak kosong
yang dilengkapi dengan dua operasi biner
yaitu operasi penjumlahan
“+”
dan operasi pergandaan “
.
” yang memenuhi
1)
(R,+
)
merupakan grup Abelian,
2)
Operasi pergandaan bersifat assosiatif,
3)
Untuk setiap
a, b, c ? R
berlaku sifat distributif kiri, yaitu
a
(b + c)
=
ab + ac
dan
sifat distributif kanan yaitu
(a + b)c =
ac + bc .
Gelanggang
(R,+,·) dapat dituliskan dengan R apabila operasi binernya diketahui.
Jelas bahwa pada
gelanggang R
memuat elemen
identitas terhadap operasi
penjumlahan yaitu
0
?
R
sedemikian hingga
a
+
0 = 0 + a =
a
, untuk setiap
a
?
R
.