51
p
p
Contoh 2.1.4.6. (Buchmann, 2000)
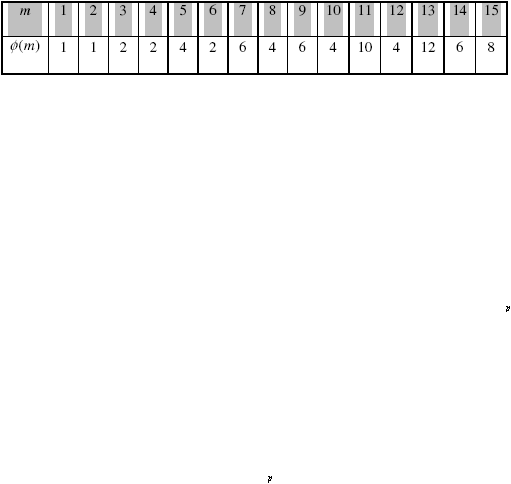
Tabel 2.4. Beberapa nilai Euler ?-function
Dari Tabel 2.4, diperoleh bahwa
?
(1) = 1
,
?
(2) = 1
,
?
(3) =
2
,
dan seterusnya. Artinya,
order dari
(Z
2
,*
)
adalah 1, order dari
(Z
3
,*
)
adalah 2, dan seterusnya.
Teorema 2.1.4.8. (Buchmann, 2000) Jika p adalah bilangan prima, maka ?
(
p) = p - 1 .
Bukti:
Diberikan
sebarang
bilangan
prima
p.
Menggunakan
Teorema
2.1.4.6
maka
(Z
,+,·
)
adalah lapangan dengan order p. Selanjutnya, dapat dibentuk grup
(Z
,*
)
yang ordernya
dinotasikan dengan
?
(
p) . Karena
Z
p
adalah
lapangan,
maka setiap elemen
tak
nolnya
pasti
mempunyai
invers, dengan kata
lain ada sebanyak
p
-
1
elemen
yang
mempunyai
invers, yang semuanya menjadi anggota
(Z
,*
). Dengan demikian diperoleh bahwa
order
(Z
,*
)
adalah
p
-
1
, terbukti bahwa
?
(
p) = p - 1
.
Pada Teorema 2.1.4.8 diketahui bahwa jika p adalah bilangan prima, maka
?
(
p) = p - 1 . Di bawah ini diberikan sebuah teorema tentang Euler ?-function.
Teorema 2.1.4.9. (Buchmann, 2000) Diberikan
bilangan
bulat
positif
m
dan
d1
,
d
2
,K, d
n
adalah semua pembagi positif m yang berbeda, maka:
n
?
?
(d
i
)
=
m
.
i
=1