25
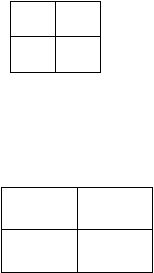
x’y’
x’y
xy’
xy
Tiap
kotak
dikatakan
bertetangga
jika minterm–minterm
yang
merepresentasikannya
berbeda hanya 1 buah literal [Kenneth H. Rosen, 2000, p612].
Peta Karnaugh dapat dibentuk dari fungsi Boolean yang dispesifikasikan dengan
ekspresi Boolean maupun fungsi yang direpresentasikan dengan tabel kebenaran.
a. Peta Karnaugh dengan Dua Peubah
Misalkan
dua
peubah
di
dalam
fungsi
Boolean
adalah
x
dan
y.
Baris
pada
peta
Karnaugh untuk peubah x dan kolom
untuk peubah y.
Baris pertama diidentifikasi
nilai
0
(menyatakan
x’),
sedangkan
baris
kedua
dengan
1
(menyatakan
x).
Kolom pertama
diidentifikasi nilai 0 (menyatakan y’), sedangkan kolom kedua dengan 1 (menyatakan y).
Setiap
kotak
merepresentasikan minterm dari
kombinasi
baris
dan
kolom
yang
bersesuaian.
Berikut
terdapat
tiga
cara
yang
lazim
digunakan
sejumlah
literatur
dalam
menggambarkan peta Karnaugh untuk dua peubah.
m
0
m1
m2
m3
Gambar 2.1 Penyajian 1 - Peta Karnaugh dengan 2 peubah
(Sumber: Rinaldi Munir, 2005, p310)
y
0
1
x
0
1
Gambar 2.2 Penyajian 2 - Peta Karnaugh dengan 2 peubah
(Sumber: Rinaldi Munir, 2005, p310)