10
Data
Dunia-nyata
perumusan
Model
Matematika
pengujian
analisis
Prediksi/
Penafsiran
penafsiran
Kesimpulan
Matematika
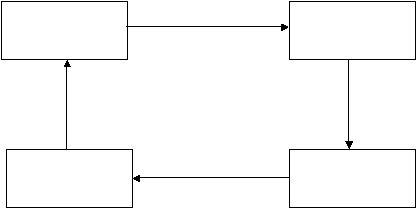
Gambar 2.1 Bagan Proses Pemodelan Matematika
(Sumber: Vries, tanpa tahun, slide6)
Dari
bagan
di
atas,
dapat
disimpulkan bahwa
proses
membangun model
matematika tidak
pernah
berhenti,
terus
bergerak
antar
tahap-tahap itu,
untuk
menghasilkan
model
yang
lebih
baik.
Gerda
de
Vries
menegaskan
bahwa
tidak
ada
model
yang
paling
baik,
hanya ada
model
yang
lebih
baik
(Vries,
tanpa
tahun,
slide6).
Akhirnya,
model
matematika sendiri dapat didefinisikan sebagai
representasi
matematis
dari
suatu
proses,
alat,
atau
konsep,
dalam
bentuk
sejumlah peubah
yang
didefinisikan
sebagai
pengganti
dari
masukan,
keluaran,
dan
proses-proses
internal
dari
proses
atau
alat
yang
direpresentasikan, dan
serangkaian
persamaan
dan
pertidaksamaan
yang
menggambarkan interaksi antar peubah tersebut.
2.2 Persamaan Differensial
Dibandingkan
dengan pemodelan
matematika,
pengertian persamaan differensial
sudah
lebih
pasti
(Ledder,
2005,
p1).
Persamaan
differensial adalah
persamaan
matematika untuk
suatu
fungsi
tak
diketahui dari
satu
atau
beberapa
peubah
yang
menghubungkan
nilai
dari
fungsi tersebut
dengan
turunannya
sendiri
pada
berbagai