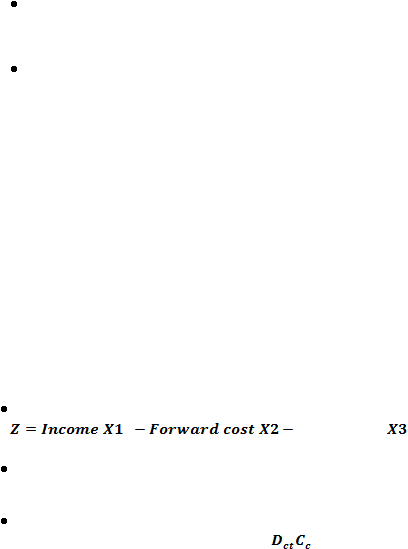
10
Asumsi ini menyatakan bahwa semua parameter yang terdapat dalam model
linear programming(a
ij
, b
ij
dan c
j
) dapat diperkirakan dengan pasti, meskipun
jarang dengan tepat.
2.4.2.
Pengertian Integer Linear Programming
Pada dasarnya integer linear programming merupakan bentuk khusus dari model
linear programming.
Integer linear programming (ILP) merupakan sebuah model
pemrograman linear bilangan bulat yang dapat menghasilkan solusi dengan nilai-
nilai baik integer dan maupun non-integer (Mulyono, 2004, p.95).
Berdasarkan ketentuan variabel keputusan yang dihadapi, ILP dapat dikelompokkan
menjadi 2 yaitu (Taha,1996, p.333) :
Pure Integer Linear Programming
(PILP) jika seluruh variabel keputusan
yang digunakan berupa bilangan bulat. Ada pula yang bernilai 0 atau 1
(boolean) dimana angka tersebut berarti keputusan dilaksanakan atau tidak.
Mixed Integer Linear Programming
(MILP)
jika variabel keputusan yang
digunakan sebagian berupa bilangan bulat dan sebagian lagi berupa bilangan
pecahan.
2.4.3.
Mixed Integer Linear Programming
Model Mixed Integer Programming
(MIP) yang digunakan dalam adalah yang
dikembangkan oleh Utami
(2010). Permasalahan yang ada diformulasikan kedalam
Stochastic Mixed Integer Linear Programming (SMILP) decision making dalam
bentuk multi stage program dengan fungsi tujuan untuk memaksimumkan
keuntungan yang diperoleh (profit).
El-Sayed et al. (2010) menjelaskan bahwa masa multi echelon forward–reverse
logistics network model
dikembangkan untuk keperluan desain di bawah risiko.
Masalahnya dirumuskan dalam stochastic mixed integer linear programming
(SMILP) pengambilan keputusan sebagai bentuk program stokastik multi-tahap.
Tujuan dari model ini adalah untuk memaksimalkan total keuntungan yang
diharapkan.
Berikut adalah Model untuk Stochastic Mixed Integer Linear
Programming.
Objective Function
Reverse Cost
(Memaksimumkan keuntungan yang didapatkan)
Total Profit
Profit = Income – Expanse Cost
Income
income =
Expanse Cost
Expanse Cost = Forward cost + Reverse Cost