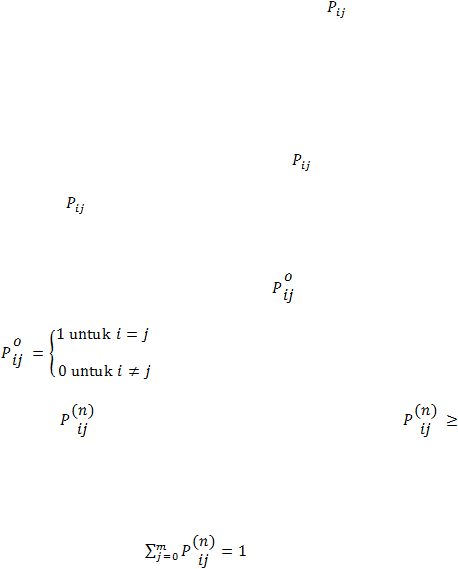
23
Markov
jika peluang bersyarat dari state
yang akan datang X
t+1
= j, jika
diberikan state
yang telah lalu dan sekarang X
t
= 1, tidak tergantung pada
state sekarang dari sebuah proses. Peluang bersyarat P(X
t+1
= j|X
t
= i) disebut
Peluang transisi.
Jika untuk setiap i
dan j
berlaku P(X
t+1
= j(X
t
= i) = P (X
t
= j|X
0
=
1)
untuk semua t = 0, 1, . . . , n
maka peluang transisi
satu langkah
dikatakan stasioner dan dilambangkan dengan
. Artinya peluang transisi
stasioner adalah peluang transisi
yang tidak berubah terhadap waktu (tidak
tergantung parameter t), sehingga untuk setiap i, j dan n, untuk n = 0, 1, . . .
, sehingga P (X
t+n
= j(X
t
= i) = P (X
n
= j|X
0
=1)
untuk t = 0, 1, . . . , n.
Peluang bersyarat ini dilambangkan oleh
dan disebut peluang transisi
n
langkah.
adalah peluang bersyarat variabel acak X
dimulai dari state i
hingga keadaan j setelah n-langkah.
Untuk n = 0 P(X
n
= j|X
0
= i) =
, dimana
Karena
adalah peluang bersyarat maka haruslah
0
untuk
semua i,j
dan n
= 0,1,….
dan karena proses membuat transisi
ke dalam
beberapa state maka :
, untuk semua i dan n = 0, 1, ….. , n
Peluang transisi dapat juga ditulis dalam bentuk matriks untuk n = 0, 1,
. . . , n :
Table 2.1 Peluang Peralihan Dalam Bentuk Matriks