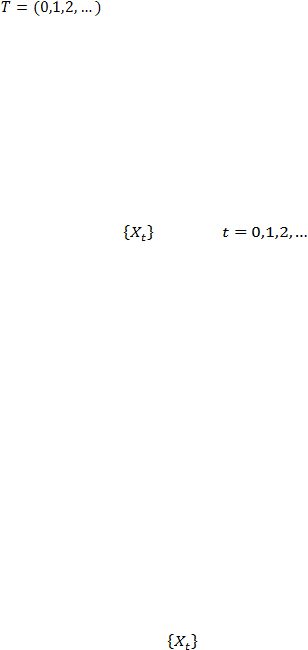
22
ini, tidak dapat dipengaruhi oleh informasi tambahan di masa yang sudah
lalu.
[Pinsky & Karlin, 2011: 79]
Rantai Markov
diskrit
adalah suatu proses Markov
yang ruang state-
nya adalah gugus hingga atau gugus yang dapat dihitung dengan gugus
indeks
. Dapat dirumuskan sebagai berikut untuk semua titik
yang berada pada waktu n dan semua state :
Pr{X
n+1
= j|X
0
= i
0
, . . . , X
n
-1
= i
n
-1
, X
n
= i}
= Pr{X
n+1
= j|X
n
= i}
pada rantai Markov
dinyatakan sebagai bilangan bulat tak
negatif, X
n
= 1 yang menyatakan bahwa X
n
terdapat pada state i.
Proses stokastik
dengan
disebut rantai Markov
state hingga jika:
1. Memiliki sejumlah hingga state
2. Bersifat Markov
3. Peluang peralihan stasioner
4. Memiliki peluang awal P (X
0
= i) untuk semua i.
[Pinsky & Karlin, 2011: 79]
Analisis Markov
merupakan suatu metode yang mempelajari sifat-sifat
suatu
variabel pada masa sekarang yang didasarkan pada sifat-sifatnya di masa
lalu dalam usaha menaksir sifat-sifat variabel yang sama di masa yang akan
datang.
Sebuah proses stokastik
dikatakan mempunyai sifat Markov
jika
peluang bersyarat dari kejadian yang akan datang P (X
t
= j|X
t
= i)
disebut
peluang peralihan. Dapat diartikan bahwa proses stokastik mempunyai sifat
(2.1)