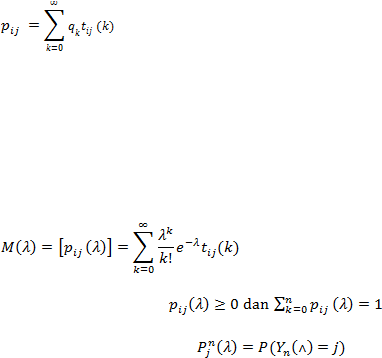
26
bahwa C1,C2,… adalah tarif grup dari tahun ke tahun dari pemegang polis. Tarif
grup tahun sebelumnya dengan banyaknya klaim yang tercatat. Dengan demikian
maka permasalahan sistem Bonus-Malus
dapat dipandang sebagai model rantai
Markov. Dengan menggunakan teori Markov, maka {C
n
} barisan peubah acak
dengan ruang tarif
grup berhingga. {C
n
} adalah Rantai Markov
yang memiliki
matrik M=(p
ij
)
sedemikian hingga untuk semua n = 1,2,… dan i
0
,i1,…,i
n
,
Pr(C
n
= i
n
| C
n-1
= i
n-1
,…., C
0
= i
0
)
= P(i
n-1
,
i
n
)
(2.9.2)
Dimana,
Pr(C
n-1
= i
n-1
,…., C
0
= i
0
) > 0
Peluang transisi p
ij
merupakan peluang perpindahan dari tarif grup ke-i
ke tarif
grup ke-j dari pemegang polis dapat dituliskan sebagai
Banyaknya klaim (k) yang terjadi dan tercatat oleh pemegang polis
diasumsikan memenuhi definisi proses Poisson
dengan laju ?. Dengan
menggunakan persamaan (2.9.1) maka matrik transisi p
ij
dari rantai Markov dapat
menjadi
Dengan,
Misal didefinisikan :
Dari persamaan (2.9.2) peluang untuk tidak ada klaim adalah positif, P
0
(?) < 0.
Dengan menggunakan sifat dari rantai Markov yang regular maka diperoleh
i.
Jika distribusi peluang untuk banyaknya klaim selama satu periode adalah
saling bebas terhadap periode, maka tarif grup untuk polisnya berbentuk