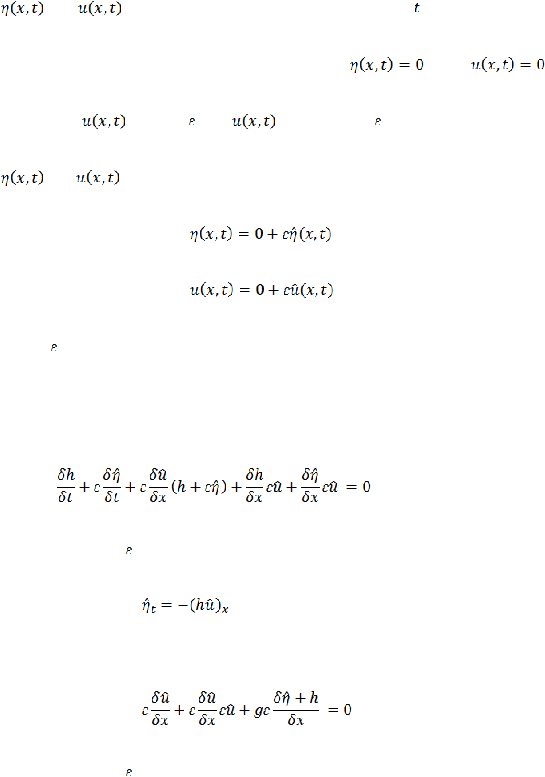
27
2.1 dan 2.2 diketahui sebagai persamaan air dangkal. Kedua persamaan tersebut akan
dilinierkan supaya lebih mudah untuk dipelajari.
Untuk melinierkan kedua persamaan tersebut, diperlukan solusi equilibrium
dan
, yaitu solusi yang tidak mengandung unsur
. Solusi equilibrium
yang memenuhi persamaan air dangkal adalah
dan
.
Dimisalkan
berorde
dan
juga berorde
sehingga expansi adalah
dan
di sekitar equilibrium adalah seperti berikut:
(2.3)
(2.4)
dengan
adalah sebuah bilangan yang sangat kecil.
Substitusikan persamaan 2.3 dan persamaan 2.4 ke dalam persamaan 2.1,
sehingga diperoleh
(2.5)
Suku-suku berorde
pada persamaan 2.5 memberikan persamaan berikut:
(2.6)
Kemudian substitusikan persamaan 2.3 dan 2.4 ke persamaan 2.2 sehingga diperoleh
(2.7)
Suku-suku berorde
pada persamaan 2.7 memberikan persamaan berikut: