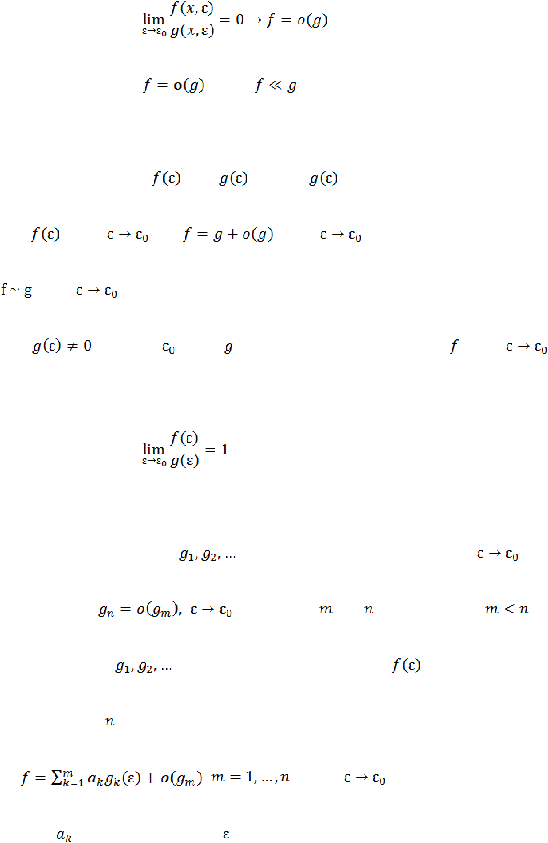
29
(2.12)
Notasi lain untuk
adalah
.
Defisini 2: Diberkan
dan
. Fungsi
dinamakan hampiran asimtotik
dari
untuk
jika
untuk
. Pada kasus ini dapat ditulis
untuk
.
Jika
di sekitar
, maka
adalah hampiran asimtotik dari
untuk
dapat ditulis sebagai
(2.13)
Definisi 3:
Barisan fungsi
dinamakan barisan asimtotik untuk
jika
dan hanya jika
untuk setiap
dan
yang memenuhi
.
Definisi 4:
Jika
adalah barisan asimtotik maka
memiliki ekspansi
asimtotik untuk
suku yang berkatian dengan barisan tersebut jika dan hanya jika
,
dengan
(2.14)
Dimana
tidak bergantung pada
. Pada kasus ini, dapat ditulis