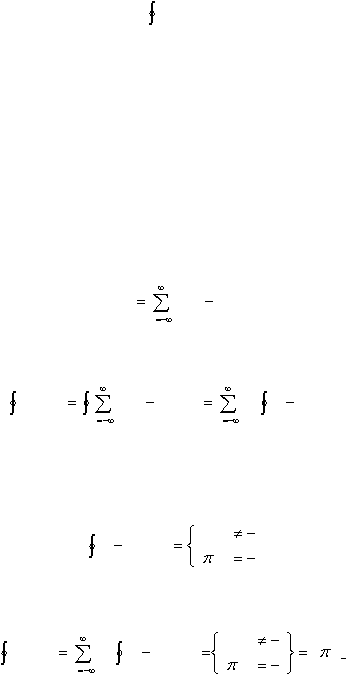
33
Misalkan f(z) adalah fungsi kompleks yang bernilai tunggal dan analitik di dalam
dan pada suatu daerah R, kecuali di titik singularnya.
Tujuan kita adalah menhitung
integral berikut
0
)dz
(z
C
f
(2.26)
dimana C
0
adalah lingkaran yang pusatnya di z
0
, dimana f memiliki singularias di
titik pusat tersebut. Asumsikan bahwa jari-jari C
0
cukup kecil sehingga fungsi f tidak
memiliki titik singular yang lain. Asumsikan pula bahwa arah C
0
berlawanan dengan
arah jarum jam.
Di sekitar titik z
0,
f(z) dapat dinyatakan sebagai deret Laurent yang diberikan
oleh
k
k
k
z
z
a
z)
f
)
(
(
0
(2.27)
Dengan demikian, persamaan (2.26) dapat dituliskan sebagai berikut
k
C
k
k
C
k
k
k
C
dz
z
z
a
dz
z
z
a
dz
z)
f
0
0
0
)
(
)
(
(
0
0
(2.28)
Ingat bahwa dengan menggunakan teorema integral Cauchy, kita dapat memperoleh
1
,
2
1
k
,
0
)
(
0
0
k
i
dz
z
z
C
k
(2.29)
Substitusikan (2.29) ke dalam (2.28) diperoleh
1
0
2
1
,
2
1
k
,
0
)
(
)dz
(z
0
0
ia
k
i
dz
z
z
a
f
k
C
k
k
C
(2.30)
Hal ini menunjukkan bahwa koefisien a
-1
dalam deret Laurent dari fungsi f di
sekitar titik z
0
menentukan nilai integral f atas lingkaran cukup kecil yang berpusat di
z
0
. Nilai a
-1
disebut residu f di z
0
, dan dilambangkan dengan Res
z0
(f).