30
X2
0
1
-3/5
-4/5
3/5
0
6/5
-
S2
0
0
1
1
-1
1
1
1
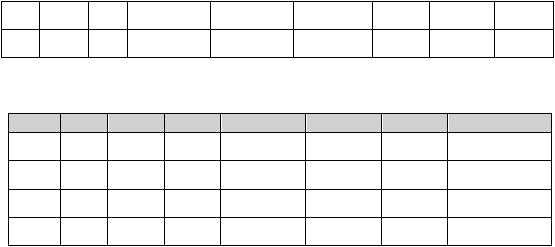
Iterasi - 3 -> Optimal
VB
X1
X2
S1
A1
A2
S2
Solusi
z
0
0
0
7/5-M
-M
-1/5
17/5
X1
1
0
0
2/5
0
-1/5
2/5
X2
0
1
0
-1/5
0
3/5
9/5
S1
0
0
1
1
-1
1
1
Contoh Penggunaan metode BIG M
pada fungsi tujuan maksimisasi
(sumber:
tanggal 20 September 2013):
Maximise
:
3X1 + 4X2
Subject to
:2X1 + X2 <= 600
X1 + X2 <= 225
5X1 + 4X2 <= 1000
X1 + 2X2 >= 150
X1, X2 >= 0
Solution:
Standard form:
Maximise 3X1 + 4X2
Subject to 2X1 + 3X2 + S1 = 600
X1 + X2 + S2 = 225
5X1 + 4X2 + S3 = 1000
X1 + 2X2 - S4 = 150
X1 , X2 , S1 , S2 , S3 , S4 >= 0
Not in canonical form because there is no basic variable in the fourth
equation.
Therefore we add an artificial variable to that equation (R1) and
give it a large
negative coefficient in the objective function, to penalise it:
Maximise 3X1 + 4X2