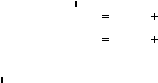
15
sehingga
meminimalkan
atau
memaksimalkan
suatu
fungsi
matematis
yang mengekspresikan kriteria perancangan tersebut.
4. Model–model state
variabel
biasanya diperlukan untuk simulasi
(solusi
persamaan diferensial dengan digital komputer).
Bentuk
baku
persamaan
state
space
dari
suatu
sistem
analog
linier
time invariant
(LTI) sebagai berikut :
x(t )
Ax(t )
Bu(t )
y(t )
Cx(t )
Du(t )
(2–13)
Dengan
x(t )
merupakan
turunan
terhadap
waktu
dari
vektor
x(t).
X(t)
merupakan
suatu
vektor
dari
keadaan-keadaan suatu
sistem
orde
n.
A
merupakan matriks sistem dengan dimensi (n x n). B
merupakan matriks
masukan
dari
suatu
sistem.
U(t)
merupakan
vektor
masukan
yang
tersusun
dari fungsi–fungsi masukan sistem.
Y(t) merupakan vektor keluaran suatu
sistem yang
terbentuk dari keluaran–keluaran
yang ditentukan. C
merupakan
matriks
keluaran.
Sedangkan
D
merupakan
suatu
matriks
yang
menunjukan
kaitan langsung antara masukan dan keluaran.
Dengan mengacu pada kedua persamaan matriks (2-13) sebagai
persamaan–persamaan
keadaan
dari
suatu
sistem, persamaan
pertama
disebut persamaan keadaan dan persamaan kedua disebut persamaan
keluaran.
Persamaan
pertama
(persamaan
keadaan)
adalah sebuah
persamaan diferensial matriks orde satu dan vektor keadaan x(t) adalah
solusinya. Dengan diberikan data x(t) dan
vektor
masukan
u(t),
persamaan
pengeluaran menghasilkan keluaran y(t).