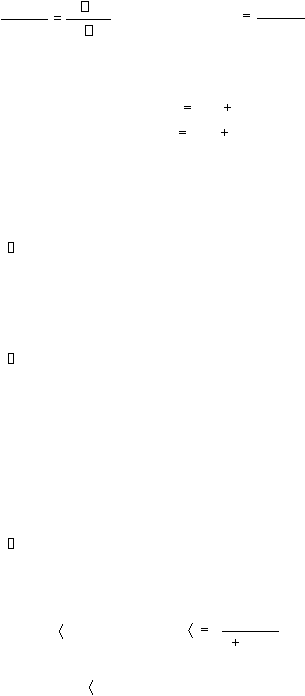
12
Persamaan
garis
yang
melalui
titik
(x1,
y1)
dengan
gradien
m
memiliki
persamaan umum y – y1 = m (x – x1).
Untuk garis yang melalui P (x1, y1) dan Q (x2, y2) memiliki persamaan :
y
y1
y2
y1
x
x1
x2
x1
, dengan gradien
m
y2
y1
...................................(2–10)
x2
x1
Bila
terdapat dua buah
garis didalam persamaan
garis,
yaitu
misalkan garis
g dan l, dengan garis
g : y
m1 x
n1
l
:
y
m2 x
n2
Maka terdapat beberapa kemungkinan hubungan yang terjadi antara 2 garis
tersebut :
Saling sejajar
Garis g sejajar garis l, bila m1 = m2
Garis g berimpit garis l, bila m1 = m2 dan n1 = n2
Saling berpotongan tegak lurus
Garis g perpotongan tegak lurus dengan garis l, bila m1.m2 = -1
Persamaan garis melalui (x1, y1) dan tegak lurus dengan garis
g : y = mx + n,
x + my – (x1 + my1) = 0
Garis saling berpotongan bebas
Dikatakan saling bebas bila perpotongan kedua garis membentuk
sudut
, dengan gradien
tg
m1
m2
1
m1
m2
........................................(2–11)
Sudut
dipilih dari perpotongan kedua garis
yang
membentuk sudut
paling kecil.