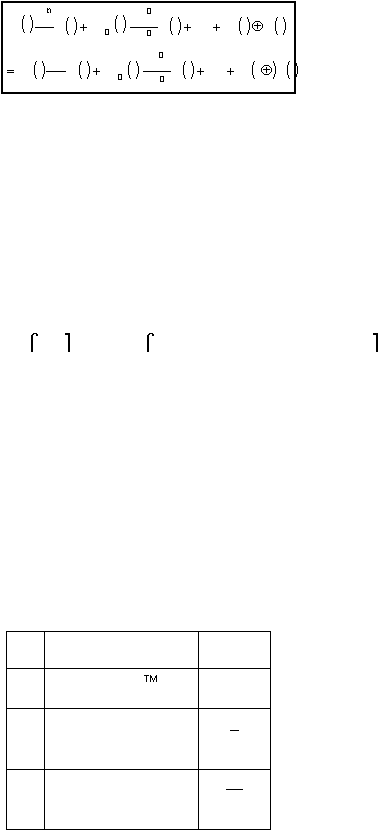
22
A
t
d
x
t
A
t
d
n
1
x
t
.....
A
t
x
t
n
dt
n
n
n
1
dt
n
1
0
n
1
........ ( Pers
2.4 )
B
t
d
y
t
B
t
d
y
t
.....
B
t
y
t
n
dt
n
n
1
dt
n
1
0
Pada
transformasi Laplace,
operasi
seperti
differensial dan
integral
dapat
digunakan dengan
operasi
aljabar
dalam
bidang
kompleks
s.
Bilangan
kompleks
mempunyai bagian
nyata
dan
bagian
imajiner, keduanya adalah konstan. Jika bagian
nyata dan
/
atau
bagian
imajiner adalah
variabel, maka
bilangan kompleks
tersebut
dinamakan
variabel
kompleks.
Pada
transformasi
Laplace
s =
+
j
,
di
mana
adalah
bagian
nyata
sedangkan
adalah
bagian imajiner.
Suatu kelebihan metode
transformasi Laplace adalah bahwa
metode ini
memungkinkan penggunaan teknik grafis untuk
meramal
kinerja
sistem
tanpa
menyelesaikan persamaan
differensial sistem.
Tabel
2.3 Transformasi
Laplace
No.
f(t)
F(s)
1
Impuls satuan
(t)
1
2
Tangga satuan 1(t)
1
s
3
t
1
s
2