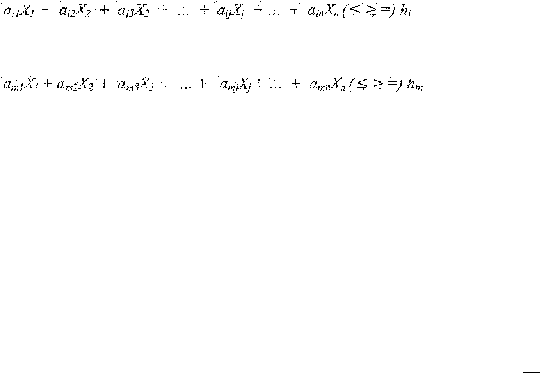
12
Pada dasamya,
pcrsoalan progra.t·n
linear dapat dirumuskan sebag.ai berikut :
Tentukan nilai XI'
x2)
xj' ·--
.Xj,,,,,
x;,
sedemikian mpa
schillgga
Z = C1X 1 +
C.t-.¥2
+
Cy(3
I
...
+
C_0j
!
...
+
Cn-X,
=
optimcun
(maksimum atau
minimum)
Deneau batasan I kendala :
auX 1
-!
a12X, + a13X3
+
a21X1
+
a11X2
-+
anA]
+
+
aljxre:-.
-!
a?JX;
+
+
a1nXn ($ =) h1
+
11],Xn (
=) h2
·VeJ O,j1.2... ,
n
Ada n
mac am barar..g
yang akan
diprodnksi
masing- masing sebcsar
X"
X
2,
X],0.... ,X,,.
n
=
banyaknya jeni.s
atau
tipe barang yang ahm diproduksi.
).;;: = banyaknyajumlah banmgjenis kc-
j
yang Ciproduksi.j "'-
1,2,3, ...
,
n
Cj= harg<t per satuan
barangjenis
ke-
j.
Adam maca.."ll
hahan me:1tah,
masing-
masing tersedia h1
,
h², ...
h,
)1m
nz
=
banyalmya jenis bahan
baku yang diperlukan U!ltuk
produk.si.
h;
=
banyaknya hahan
mentah kc
-
i yang tersl'"fdia.
au
=
banya..l.;:nya
bahan
mcntah
ke
-
i
yang
digunakan
tL."1tuk
memproduksi
satu
satuan barang
jenis ke-
j.