43
mempermudah
analisa.
Pembagian
tersebut
memungkinkan
sistem
yang
memiliki
derajat
kebebasan
tak
terhingga
dapat
didekati
menjadi
suatu
sistem yang
memiliki
derajat kebebasan berhingga. Semakin kecil elemen terbagi yang digunakan dalam
analisa maka semakin akurat hasil yang diperoleh melalui analisa tersebut, selama
elemen kecil ini tidak mengalami putus di suatu tempat.
Dalam metode
elemen
hingga,
wilayah
model
didiskretisasi
menjadi
elemen-
elemen, baik dengan
jarak teratur
maupun
yang
tidak teratur.
Dalam diskretisasi, benda
dibagi
menjadi beberapa
elemen
dengan bentuk
yang
teratur pada bagian dalam. Jenis
elemen
yang
akan
digunakan
tergantung
pada karakteristik rangkaian kesatuan dan
idealisasi.
Sebagai
contoh,
jika
suatu
struktur diidealisasi
sebagai
suatu
garis
satu
dimensi, elemen yang digunakan adalah suatu elemen garis. Untuk benda dua dimensi,
digunakan jenis elemen segitiga dengan tiga atau enam titik nodal atau segiempat
dengan empat atau lebih titik nodal dan
untuk obyek idealisasi tiga dimensi digunakan
jenis
elemen
segienam
(heksahedron)
dengan
kekhususan
yang
berbeda.
Secara
umum
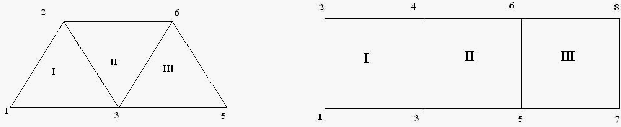
bentuk aplikasi dari elemen tersebut dapat dilihat pada gambar 2.16.
Gambar 2.15. Aplikasi Elemen Segitiga dan Elemen Segiempat
(Sumber : C.S. Desai, 1988)