19
?
N
-
dI
=
aSI - ßI .
(2-3)
dt
Dua
persamaan (2-2)
dan (2-3)
membentuk satu
model
matematika
yang biasa disebut
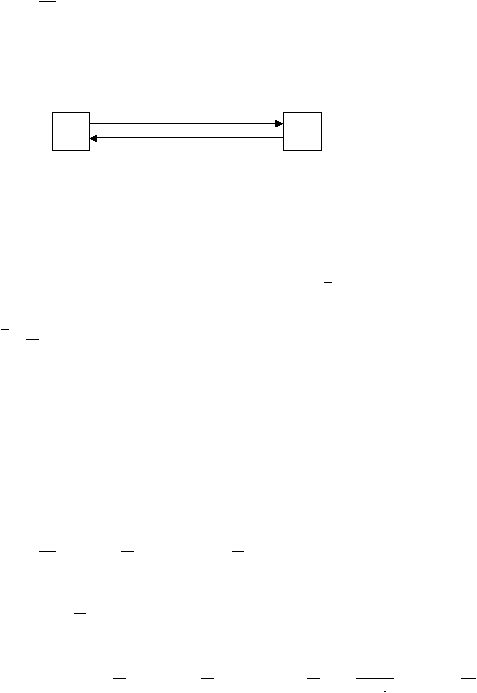
dengan model SIS. Berikut ini diagram yang merepresentasikan model ini.
aSI
S
I
ßI
Gambar 2.2 Diagram model SIS
(sumber: Robeva, 2008, p61)
Laju kesembuhan per orang ß pada model SIS ini berhubungan dengan lama rata-
rata seorang terjangkit penyakit
ini, dilambangkan dengan d
.
Hubungannya dinyatakan
dengan:
d
=
1
.
Jadi,
makin kecil
nilai ß,
makin
lama
jangka
waktu rata-rata penyakit
ß
ini menjangkiti seseorang.
Dengan berjalannya waktu, perilaku jangka panjang penyakit
menular
ini dapat
dimodelkan sebagai berikut.
Berdasarkan kondisi S(t) + I(t) = N, persamaan (2-3) dapat ditulis dengan:
dI
?
ß
?
?
ß
?
=
aI
?
S
-
?
=
aI
?
N
-
I
-
?
.
dt
?
a
?
?
a
?
Berikutnya, jika N -
ß
> 0 , sisi kanan persamaan di atas dapat ditulis sebagai:
a
?
ß
?
?
?
?
ß
?
?
?
?
?
aI
?
N
-
I
-
?
=
aI
?
N
-
B
-
I
?
= ß
?
N
-
?
?
1
-
I
?
I
=
r
?
1
-
I
?
I
,
?
a
?
?
a
?
?
a
?
?
=
ß
?
a
?
?
K
?