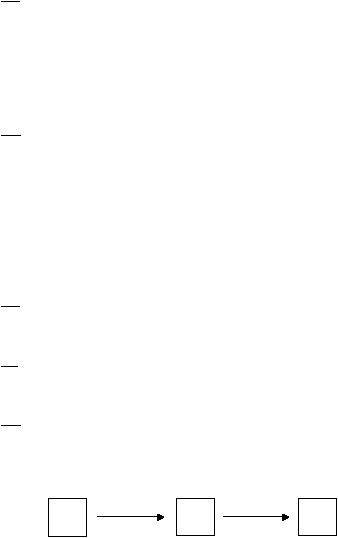
22
R
Selanjutnya diperlukan persamaan-persamaan
yang
menggambarkan
perubahan
pada
masing-masing kelompok. Sebagaimana
model SIS, diandaikan bahwa
laju
infeksi
adalah aSI,
namun pada
model SIR
tidak ada arus kembali ke dalam kelompok S, karena
mereka yang telah sembuh menjadi kebal. Oleh karena itu, persamaan differensial yang
pertama akan berbentuk:
dS
=
-aSI .
dt
Individu
yang sembuh dari penyakit akan bergabung pada kelompok R.
Jika diandaikan
bahwa angka kesembuhan perorang adalah ß, laju perubahan pada kelompok R adalah:
dR
=
ßI .
dt
Kelompok I,
menerima perpindahan dari kelompok S sebesar aSI dan
melepaskan
menuju
kelompok
R
sebesar
ßI.
Menggabungkan
laju
perubahan
dari
ketiga
kelompok
penyusun model SIR ini, didapatkan sistem persamaan differensial berikut ini.
dS
=
-aSI
dt
(2-4a)
dI
=
aSI - ßI
dt
(2-4b)
dR
=
ßI .
(2-4c)
dt
Berikut ini diagram yang merepresentasikan model ini.
S
aSI
I
ßI
Gambar 2.3 Diagram model SIR
(sumber: Robeva, 2008, halaman 66)