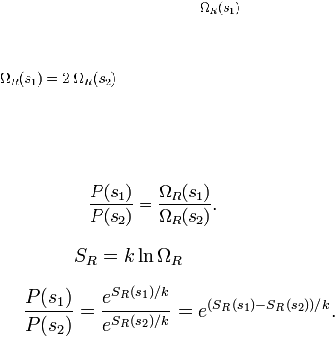
20
2.5.1.1
Distribusi Maxwell – Boltzmann
Distribusi statistik Maxwell-boltzmann menggunakan pandangan klasik, dimana
sesuai dengan asumsi :
1. Partikel penyusun dapat dibedakan
2. Dalam satu keadaan energy dapat diisi oleh lebih dari satu partikel
Fungsi
distribusi
Boltzmann
didapatkan
secara
langsung
dari
analisis
pengembangan
dari sebuah
sistem.
Selama
energinya bebas
untuk
mengalir
antara sistem
dan partikel,
partikelnya akan
mempunyai kapasitas panas
yang besar
untuk
memperbaiki
temperatur
konstan,
T,
untuk
sistem
yang
dikombinasikan. Dalam konteks
ini,
sistem diasumsikan
memiliki
tingkat
energi
e
i
dengan
degenerasi
g
i
.
Seperti
sebelumnya,
probabilitas
akan
dihitung dari sistem yang memiliki energi e
i
.
Jika sistem ada dalam state S1, maka akan ada angka sesuai dari microstate yang
tersedia
kedalam
partikel.
Anggap
angka
itu
.
Asumsikan,
kombinasi
sistem
di
isolasi,
jadi
semua
microstate
akan
memiliki
kemungkinan yang
sama
besar.
Maka,
singkatnya
jika
,
dapat
di
simpulkan
bahwa
sistem
yang
ada
dua
kali
lebih besar
di
state
S1 daripada S2
.
Umumnya, P(S
i
)
adalah probabilitas sistem berada di
state S
i
.
(2.19)
Karena entropi dari partikel
, pernyataan diatas menjadi
(2.20)
Selanjutnya
ada
yang
disebut
identitas thermodinamika ( dari
hukum
pertama
thermodinamika) :