9
2.1.3
Uji Asumsi Residual
Apabila dalam analisis regresi tidak didasarkan pada asumsi residual, maka
akan mengakibatkan hasil pendugaan regresi tidak sesuai. Asumsi residual dalam
model regresi harus memenuhi kriteria identik, independen, berdistribusi normal
(Manurung, 2007: 66-70). Pemodelan regresi klasik dengan Ordinary Least Square
(OLS) sangat ketat terhadap beberapa asumsi. Apabila ada asumsi yang tidak
terpenuhi, maka terdapat indikasi adanya pengaruh spasial (Andra, 2007: 52).
Untuk melakukan analisis regresi diperlukan asumsi-asumi
residual
yang
harus dipenuhi di antaranya adalah :
1.
Asumsi identik merupakan salah satu asumsi residual yang penting dari model
regresi. Varians residual harus bersifat homoskedastisitas atau varians residual
bersifat identik
tidak
membentuk
pola
tertentu. Beberapa uji yang dapat
digunakan untuk menguji asumsi identik adalah uji Glejser, park test, plot of
residual and fit.
Hipotesis untuk uji Glejser adalah sebagai berikut:
H
0
:
residual identik
H1: residual tidak identik
Statistik Uji:
MSE
MSR
F
hitung
(2.3)
dimana :
k
e
e
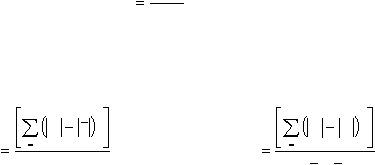
MSR
n
i
i
1
2
ˆ
;
1
ˆ
1
2
k
n
e
e
MSE
n
i
i
i