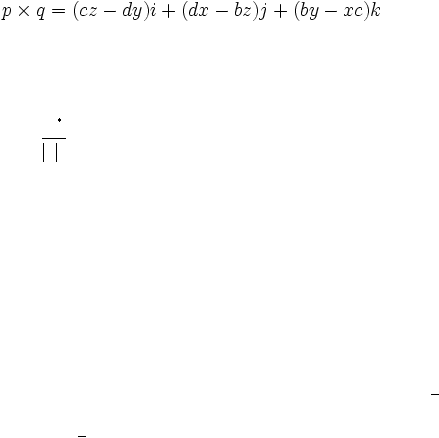
17
2
-
Perkalian cross
-
Invers
p
-1
=
p
p
(
pq
)
-1
= p
-1
q
-1
2.2.4.2 Penggunaan Quaternion Dalam Rotasi
Bentuk umum Quaternion : q= (a + bi + cj + dk
)
Titik di ruang 3D dengan bentuk quaternion adalah p(0,x,yz
)
=
0+xi+yj+zk , sehingga
jika ingin merotasikan titik dengan menggunakan quaternion maka
p
rotated
=
qpq
-1
, karena q adalah unit quaternion , sehingga
q
-1
=
q
untuk operasi *.
p
rotated
=
qpq
p
rotated
=
(-bx-cy-dz+i
(
ax + cz- dy) + j (ay - bz + dx) + k (az + by - cx ) )*(a- bi - cj -
dk)
p
rotated
=
(- bx -cy- dz)*a - ( ax + cz- dy)*(-b) -(ay - bz + dx)(-c) - (az + by - cx )*(-d)
+
i
((
ax
+
cz-
dy)(a)
+
(-
bx
-c
y-
dz)(-b)
+
(ay
-
bz
+
dx)(-d)
-
(az
+
by
-
cx
)(-c)
)
+
j
((-
bx
-c
y-
dz)(-c)
-
(
ax
+
cz-
dy)(-d)
+
(ay
-
bz
+
dx)(a)
+
(az
+
by
-
cx
)(-b))
+ k ((- bx -cy- dz)(-d) + ( ax + cz- dy)(-c) - (ay - bz + dx)(-b) + (az + by - cx )(a))
p
rotated
=
-
bax
–
cay
–
daz
+
abx
+
cbz
–
dby
+
acy
-
bcz
+
dcx
+
adz
+
bdy
-
cdx
+ i ( aax + caz- day + bbx +cby+ dbz - ady + bdz - ddx + acz + bcy – ccx)