23
2.2.1.3 Matriks Transformasi Homogeneous
Berdasarkan
Fu,
Gonzales
dan
Lee
(1987,
p27-29)
berikut
bagian-bagian
yang
penting
tentang
transformasi
homogeneous.
Matriks
rotasi
3x3
yang
sebelumnya
tidak
dapat
digunakan
untuk
menunjukkan pergeseran
dari
suatu
posisi
(translasi)
dan
penskalaan, untuk
itu
dibutuhkan sebuah
matriks
baru
yang
bisa
merepresentasikan
pergeseran sekaligus penskalaan. Matriks
transformasi homogeneous
merupakan sebuah
matriks
4x4
di
mana
matriks
ini
dapat
memetakan sebuah
vektor
posisi
yang
diekspresikan dalam
koordinat
homogeneous
dari
suatu
sistem
koordinat
ke
sistem
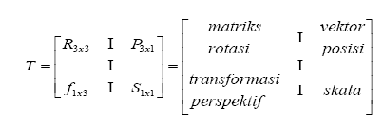
koordinat lainnya. Sebuah matriks transformasi homogeneous terdiri dari 4 submatriks:
Pers.......(2-5)
Submatriks 3x3
yang terletak di kiri atas
merepresentasikan
matriks rotasi,
submatriks
3x1
di
bagian
kanan
atas
merepresentasikan vektor
posisi
dari
system
koordinat asal
yang dirotasi
mengacu pada sistem koordinat referensi. Submatriks 1x3 di
bagian
bawah
kiri
merepresentasikan
transformasi
perspektif,
dan
terakhir
submatriks
1x1
yang
terletak
di
bagian
kanan
bawah
adalah
matriks
yang
merepresentasikan
factor
penskalaan. Selanjutnya
sebuah
matriks
rotasi
3x3
bisa
diperluas
menjadi
matriks
transformasi homogeneous 4x4 yang dilambangkan dengan Tr
ot
.
Pada
Persamaan
(2-1)
sampai
dengan persamaan
(2-3)
dapat
diekspresikan
sebagai matriks transformasi homogeneous,